
Аннотация: В статье описан принципиально новый метод представления чисел, с помощью которого возможно решить проблему потери данных при умножении на ноль и получения неопределённости при делении на ноль.
Ключевые слова: деление на ноль; оперирование бесконечностью; многомерные числа
Введение
Исторически «ноль» является проблемой в математике: с одной стороны, без ноля невозможно представить современную математику, с другой использование ноля накладывает некоторые ограничения в расчётах (например, деление на ноль).
Актуальность
В большинстве случаев математики и программисты смирились с неудобствами в расчётах, связанных с нолём, получение неопределённости при делении на ноль и потеря данных при умножении на ноль.
Новый метод представления чисел может дать возможность «не смирившимся» делить и умножать на ноль и бесконечность бесконечно много раз и при этом не «терять» результат расчётов.
Научная новизна
Предлагаемое принципиально новое понимание ноля и бесконечности, может раскрыть, для научного мира множество парадоксов и решить до сего момента не решённые задачи.
История ноля и его представление в современной математике
Понятие ноля и бесконечности в истории отлично описана Чарльзом Сейфе [1].
Современное понимание ноля и бесконечности:
Ноль - это «портал» в другие миры
Те, кто из нас помнят начальную школу могут сказать, что там нас учили, что 0 — это пустота или отсутствие чего-либо. Если у Тани 0 яблок, а у Саши 5 яблок, сколько у Тани и Саши яблок?
\( 0 + 5 = 5 ; \)
Нет сомнений, ни у кого не может быть меньше 0 яблок.
Первый портал ноля
Но потом, в средней школе оказалось, что существуют числа меньше ноля.
Появление отрицательных чисел стало логическим продолжением оператора вычитания «-», когда из меньшего числа мы вычитаем большее, само появление отрицательных чисел никого не смутило (за малостью лет мы не задали вопрос Марье Ивановне, мол, а как может быть у Тани меньше 0 яблок), и мы приняли это как данность, и пошли дальше.
Второй портал ноля
Вроде всё ясно, числа могут быть положительными и отрицательными (ты можешь быть в прибыли, а можешь получить убыток), и мы все с этим смирились.
Но вот оказалось, что всё не так просто:
Возведение в степень и извлечение корня из отрицательного числа не давали однозначных решений, и тогда появилась гениальная теория мнимых чисел, она всё нам объяснила.
Корень из отрицательного числа может быть как положительным, так и отрицательным (это число назвали мнимым, оно и существует и нет одновременно).
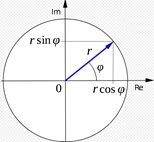
Прекрасно, мнимые числа описаны Марком Беньевичем Балк [2].
Вроде всё понятно, но…
Третий (крайний) портал ноля
Что делать, когда нам приходиться делить на ноль?
Всё что нам объяснили в школе (кроме примера с калькулятором) так-то что при делении на ноль получается «бесконечность».
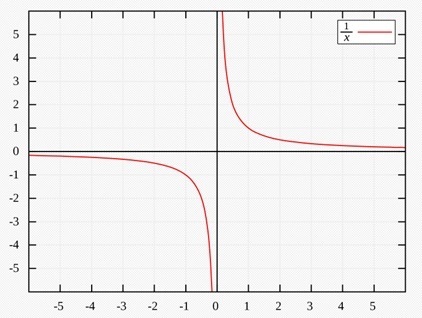
Бесконечность? А что это такое? Это не число! Это то что поглощает любые числа, все числа делятся на все, кроме ноля, поделив на ноль мы получаем «бесконечность», то есть «не число»!
Те, кто учился в институте могут вспомнить ещё вот эту картинку:
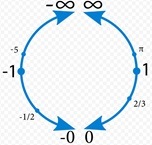
Но нам никто не рассказал, что делать с вот этими выражениями:
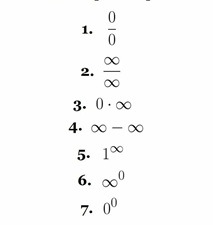
Все эти уравнения не имеют решения.
Те из нас кто глубоко изучал высшую математику ещё вспомнят вот эту картинку:
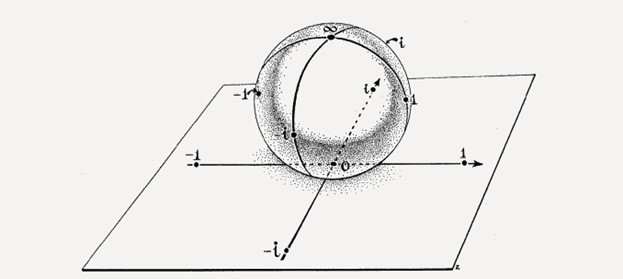
Это сфера Римана.
Которая объясняет нам проблему деления на ноль и что в итоге получается.
Прежде чем перейти к сути, немного поразмышляем:
Давайте на время забудем о том чему нас учили и попробуем ответить, на несколько вопросов про бесконечность, так как вы это понимаете на житейском уровне.
Вопросы о бесконечности:
| Что больше: | \( \infty \) или \( \infty \) ? Очевидно что они равны? Или нет? |
| Что больше: | \( \infty \) или \( \infty + 100 \) ? или они равны? Или нет? |
| А если так: | \( \infty \) или \( \infty + 10000000000000 \) ? |
| А так?: | \( \infty \) или \( \infty * 2 \) ? Так кажется точно второе значение больше? |
| А если так: | \( \infty \) или \( \infty * \infty \) ? Вот тут, то сто процентов правое выражение больше? |
Классическая математика говорит о том, что все эти выражения не имеют ответа, то есть нельзя поставить ни один из знаков неравенства.
Несмотря на то, что ниже приведённые умозаключения противоречат самому понятию "бесконечности" прошу Вас прочесть их и постараться понять.
Если представить что бесконечность имеет какой-то конечный вид, то было бы логичным заключение о том, что две бесконечности больше чем одна. А бесконечно много бесконечностей, тем более больше, чем просто бесконечность.
Оказывается, если поменять представление о бесконечности, то становиться возможным оперировать ею как обычным числом. При этом изящно решить проблемы деления на ноль и потери данных при умножении на ноль. Для того чтобы числа не растворялись в бесконечности необходимо принять постулат, что бесконечность конечна и она есть обратное от абсолютного ноля.
Многомерные числа и их представление
Для начала дадим некоторые определения, выражениям которыми будем пользоваться в дальнейшем:
Классический ноль – это тот самый ноль (в классической математике) при умножении на который любого числа мы получаем классический ноль, а при делении на него получается неопределённость (классическая бесконечность).
Классическая бесконечность – эта та самая бесконечность (неопределённость) в которой растворяются все числа при использовании её в качестве оператора.
Многомерный ноль – это любое число, делённое на бесконечность (многомерную бесконечность) в первом представлении многомерный ноль это $$ \frac{n}{\infty} = n * \infty^{-1} $$ где n - любое (классическое) число не равное классическому нулю или классической бесконечности, например, единица (в дальнейшем первоначальный ноль при автозаполнении баз данных будем представлять именно как $$ 1 * \infty^{-1} $$ . Это выражение не противоречит классической математике, т.к. любое число, делённое на бесконечность это ноль. Для понимания: в общем случае многомерный ноль это $$ n * \infty^{-m} $$ где m – целочисленное число от 1 до \( \infty \).
Многомерная бесконечность – это любое число, умноженное на бесконечность (многомерную бесконечность) в первом представлении многомерная бесконечность это $$ n * \infty^{1} $$ где n - любое (классическое) число не равное классическому нулю или классической бесконечности, например, единица (1). В общем случае многомерная бесконечность это $$ n * \infty^{m} $$ где m – целочисленное число от 1 до \( \infty \).
Число нулевого (существующего) измерения – это классическое число, которое представленное в многомерном выражении как $$ n * \infty^{0} $$
Размерность (измерение) – это целочисленное число, в степь которого возведена бесконечность в представлении многомерных чисел, функции сложения и вычитания возможны только с числами той же размерности (измерения). Размерность может быть отрицательной
И так, в общем случае, действительные числа
$$ 1 * \infty^0 \; , \; 2 * \infty^0 \; , \; 3 * \infty^0 \; , \; $$ и т.д.
Где степень, в которую возведена бесконечность говорит об измерении, в котором находится значение.
То есть, нулевая степень – значит наше обычное (классическое) измерение.
(-1) «минус первая» как и -2, и -3…. и т.д. степень говорит о том, что это значение на одно или несколько измерений ниже классического, и в представлении классической математики это ноль.
Соответственно 1, 2, 3 и т.д. степень говорит нам о том, что значение находится на одно или несколько измерений выше чем классическое и в классическом случае это бесконечность.
Для начальных условий принимаем $$ 0 = 1 * \infty^{-1} $$
Если делим на ноль любое число, то степень бесконечности увеличивается на единицу, если умножаем то уменьшается.
и получаем: $$ \frac{X}{0} = \frac{X}{1 * \infty^{-1}} = X * \infty^{1} $$ то есть обычную в нашем понимании бесконечность, но при этом число не теряется в бесконечности. А остаётся для дальнейших расчётов, и если в последующих расчётах его умножить на «ноль» $$ 1 * \infty^{-1} $$ то степень бесконечности уменьшиться, и число не будет потеряно)
Таким образом, исключается потеря данных при умножении или делении на ноль.
Многомерная арифметика (или сложение и вычитание бесконечностей с обычными числами):
Если обычное число представить как: $$ X * \infty^{0} + X * \infty^{-1} + ... X * \infty^{-n} ... X * \infty^{-\infty} $$ становиться ещё интереснее.
В программировании можно задать бесконечный список, с помощью которого можно описать вышеприведённое число.
Теперь можно вычитать и складывать бесконечность с обыкновенными числами без потери данных
Например:
|
\( 1 * \infty^{1} \) Бесконечность |
+ |
\( 20 * \infty^{0} \) Обычное число |
Машина поймёт, что к числу первого порядка прибавляется число нулевого порядка, и запишет в память, именно так: $$ ( 1 * \infty^{1} ) + ( 20 * \infty^{0} )$$ если в последующем будут прибавляться или вычитаться числа нулевого порядка, то действия сложения или вычитания буду производиться именно с нулевым порядком, то же самое относиться ко всем остальным меньшим порядкам этого числа. В общем случае: складываться или вычитаются числа соответствующих порядков.
Правила умножения и деления в многомерной арифметике такие же как в классической арифметике с умножением и делением многочленов:
результатом умножения одного многомерного числа(Х) на другое(Y), станет такое многомерное число (Z), в котором сложатся произведения каждого измерения числа (Х) с каждым измерением числа (Y) в соответствии с правилами умножения многочленов, например:
|
\( (5 * \infty^{0}) + (20 * \infty^{-1}) \) Это обычное число «5» которому уже довелось складываться с классическим нулём, который в свою очередь уже был умножен на 20 |
* |
\( (2 * \infty^{1}) + (5 * \infty^{0}) \) в обычном понимании это бесконечность, но в многомерной арифметике это две бесконечности, которым довелось суммироваться с обычным числом «5» |
получаем $$ [(5 * \infty^{0}) * (2 * \infty^{1})] + [(20 * \infty^{-1}) * (2 * \infty^{1})] + [(5 * \infty^{0}) * (5 * \infty^{0})] + [(20 * \infty^{-1}) * (5 * \infty^{0})] $$ Или: $$ 10 * \infty^{1} + 65 * \infty^{0} + 100 * \infty^{-1} $$
Деление многомерных чисел:
Деление столбиком) как в многочленах $$ \frac{(10 * \infty^{1}) + (65 * \infty^{0}) + (100 * \infty^{-1})} {(2 * \infty^{1}) + (5 * \infty^{0})} = (5 * \infty^{0}) + (20 * \infty^{-1}) $$
Получаем интересный эффект, если в процессе вычислений мы многократно складываем нули и бесконечности, делим и умножаем, то числовое значение не теряется.
Таким образом, можно число сколь угодно много раз умножить на ноль, а после этого столько же раз разделить на ноль, то мы увидим то самое число.
Реализация в программировании
Прошу прощения за синтаксис, главное понять идею, для примера использован С++.
создаём некий класс или структуру (кому как удобно), например multinumber со следующими членами:
int dimension; // степень бесконечности, по умолчанию для всех чисел кроме ноля степень бесконечности равна 0; для ноля -1.
float value; // собственно само значение числа, может быть отрицательным и положительным,
*multinumber littlenumber // указатель на следующего члена нижнего порядка многомерного числа. На начальном этапе он равен NULL.
Функции:
конструктор по умолчанию, где создаётся объект для классического ноля со следующими значениями
dimension = "-1"; value = "1"; littlenumber = NULL;
конструктор для вводимых данных, где пользователем или программой задаются значения
dimension = "Y"; value = "X"
опять таки если пользователь создаёт ноль то создаём объект по умолчанию.
деструктор в котором не забываем прописать рекуперативное удаление всех младших членов.
Ну и собственно перегружаем арифметические функции для членов этого класса(или структуры):
для "+" и "-" если степень бесконечности равны и нет младших членов то соответственно сумируем или вычитаем значение value и возвращаем с тем же значением dimension, если у слагаемых есть младшие члены то соответственно делаем с ними тоже самое. если dimension не равны, то слагаемому с большим значением степени бесконечности, добавляем littlenumber с указателем на слагаемое с меньшим значением dimension (все числа, кроме ноля по умолчанию $$ 1 * \infty^{-1} $$ , который мы просто игнорируем)
для "*" для старших членов умножаемых multinumber перемножаем value и суммируем dimension, если есть младшие члены то в возвращаемом multinumber добавляем соответствующие littlenumber в соответствии с правилами умножения многочленов.
для "/" для старших членов multinumber соответственно вычитаем dimension и соответственно делим value, если есть младшие члены то в соответствии с правилами деления многочленов делим их.
Можно также прописать функцию отображения значений для пользователя, где у нас три варианта значений
с dimension меньше ноля тогда отображаем "0";
dimension = 0; тогда отображаем value;
и dimension больше ноля тогда отображаем "infinity"
теперь подставляем вместо обычных float наш multinumber и вуа-ля, наслаждаемся делением на ноль)
эта модель работает на всех видах числовых данных, в том числе опробована на комплексных числах.
Честно признаться, младшими членами можно пренебречь и оперировать только старшими. Мне пока не довелось, встретится с задачей, где младшие члены многомерного числа играли роль, хотя допускаю, что такие задачи могут быть.
Если пренебрегать младшими членами то класс(структура) multinumber становится ещё проще.
Библиографический список
1. Чарльз Сейфе. Ноль: биография опасной идеи, 2014
2. Балк М.Б. Реальные применения мнимых чисел, 1988
С благодарностью к источнику: SCI-ARTICLE.RU
