Неравенство с одной переменной — это два выражения с переменной, соединенные знаком неравенства \((\gt; \; \lt; \; \leq; \; \geq)\).
Решением неравенств с одной переменной называется такое значение переменной, которое обращает его в верное числовое неравенство.
Решить неравенство — это значит найти все его решения или доказать, что их нет, т.е. найти множество решений неравенства.
Решением неравенства с одной переменной, как правило, является числовой промежуток или совокупность промежутков.
Числовой промежуток — это множество чисел, удовлетворяющих одному из условий, перечисленных в первом столбце таблицы.
| Числовые промежутки | Обозначение | Название |
|---|---|---|
| \(a \lt x \lt b\) | \((a; b)\) | Открытый промежуток, интервал |
| \(x \gt a\) | \((a; +\infty)\) | |
| \(x \lt a\) | \((-\infty; a)\) | |
| x — любое | \((-\infty;+\infty)\) | |
| \(a \leq x \leq b\) | \([a;b]\) | Закрытый промежуток, отрезок |
| \(a \lt x \leq b\) | \((a; b]\) | Полуоткрытый промежуток, полуинтервал |
| \(a \leq x \lt b\) | \([a; b)\) | |
| \(x \leq a\) | \((-\infty; a]\) | |
| \(x \geq a\) | \([a; +\infty)\) |
Равносильными (эквивалентами) называются неравенства, имеющие одно и то же множество решений (в частности, не имеющие решений).
Чтобы получить неравенство, равносильное данному, можно производить действия, вытекающие из свойств числовых неравенств:
- к обеим частям неравенства прибавлять одно и то же число;
- умножать обе части неравенства на одно и то же число;
- умножать обе части неравенства на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.
Схема решения неравенств первой степени (линейных) с одной переменной
| \(a \cdot x \geq b\) | |||
|---|---|---|---|
| \(a \neq 0\) |
\(a = 0\) \(0 \cdot x \geq b\) |
||
|
\(a \gt 0\) \(x \ge \frac{b}{a}\) \(x \in \left[\frac{b}{a}; +\infty\right)\) |
\(a \lt 0\) \(x \le \frac{b}{a}\) \(x \in \left(-\infty; \frac{b}{a}\right]\) |
\(b \gt 0\) нет решений |
\(b \le 0\) \( x \) — любое число \(x \in (-\infty; +\infty) \) |
В случае строгого неравенства \(ax \gt b\) схема аналогична, но все неравенства таже строгие, а интервалы — открытые.
Метод интервалов при решении неравенств
Этот метод удобен для решения неравенства вида \( P(x) \gt 0 \; (\lt; \; \geq; \; \leq) \), или \( \frac{P(x)}{Q(x)} \gt 0 \; (\lt; \; \geq; \; \leq) \),
где P(x) и Q(x) — многочлены, раскладываемые на множетели.
-
Рассмотрим неравенство \( P(x) \gt 0 \), и пусть многочлен \( P(x) \) раскладывается на множетели следующим образом:
\(P(x)=(x-x_1)(x-x_2)...(x-x_n) \gt 0\) , где \(x_1, x_2, ...x_n\) – корни данного многочлена и \(n \geq 2\).Предположим, что все эти корни разные.
Знак левой части неравенства зависит от комбинации знаков линейных множителей и меняется в каждой из точек \(x_1, x_2, ...x_n\).
Допустим, что \(x_1 \lt x_2 \lt x_3 \lt ... \lt x_n\).
При \(x \gt x_n\) все линейные множетели положительны, и вся левая часть тоже.
При \(x_{n-1} \lt x \lt x_n\) меняет знак только последний множитель, значит, и все выражение отрицательно.
При \(x_{n-2} \lt x \lt x_{n-1}\) отрицательны два последних множителя, значит левая часть опять положительна (т.к. «минус» умножить на «минус» получим «плюс») и т.д.Эти рассуждения позволяют сразу найти все решения неравенства, если воспользоваться числовой прямой.
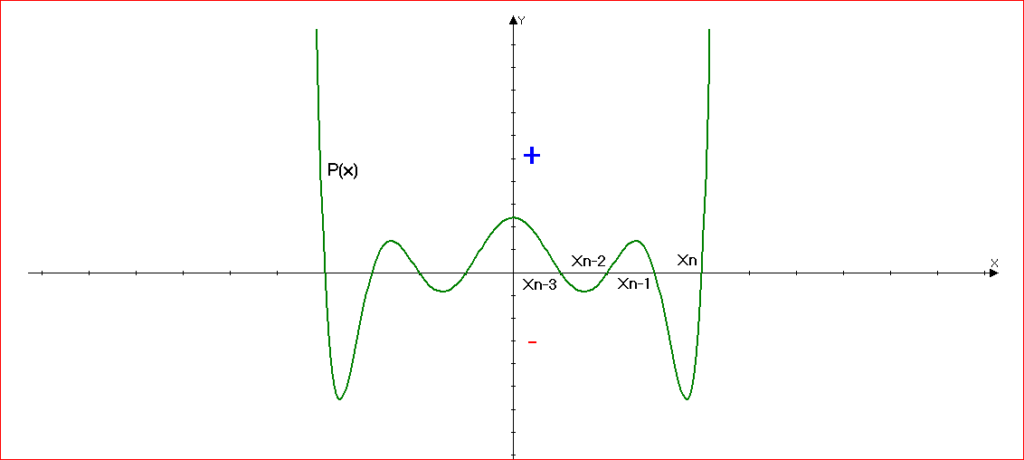
отметим на числовой прямой числа \(x_1, x_2, ...x_n\) и проведём через них кривую (как показано на рисунке).В общем виде нельзя показать, как эта кривая пересечет прямую в точках \(x_1 и x_2\), т.к. мы не знаем, четно или нечетно n.
Если кривая проведена именно таким образом, то участки кривой, лежащие над числовой прямой, соответствует решению неравенства \(P(x)\gt 0\),
а участки кривой, лежащие под осью – решение неравенства \(P(x)\lt 0\),
(в случае строго неравенства берутся открытые промежутки, в случае нестрого — закрытые).Так в нашем случае:
\(P(x)\gt 0\) при \(x \in ...(x_{n-2};x_{n-1})\bigcup{(x_n;+\infty)} \)
\(P(x)\leq 0\) при \(x \in ...[x_{n-3};x_{n-2}]\bigcup{[x_{n-1};x_n]} \)Пример
\( x(x-4)(x+8)(x-1,5)(2x+6)\geq 0 \)
при \(x \in [-8; -3] \bigcup [0; 1.5] \bigcup [4; +\infty) \) -
Пусть теперь среди множителей встречаются одинаковые (кратные).
Их произведение тогда можно записать с помощью степени в виде \((x-a)^2\) или \((x+b)^3\) и т.д.Если в разложении P(x) входит множитель вида \((x-a)^m\), где m нечетно,
мы можем заменить его при решении неравенства множителем \((x-a)\), т.к. у них знак один и тот же.Если в разложении P(x) входит множитель вида \((x-a)^m\), где m четно,
то в нестрогом неравенстве его можно просто опустить, т.к. он положителен и никак не влияет на знак.
В случае строгого неравенства просто опустить множитель \((x-a)^2, \;\; (x-a)^4\) и т.д. нельзя,
т.к. мы должны включить в множество решений неравенства точку \(x=a\), для которой \(P(x)=0\).Пример
-
\( x(x-3)^3 \cdot (x-5) \gt 0 \)
т.к. корень x = 3 имеет кратность 3 (нечетная), то знак меняется.
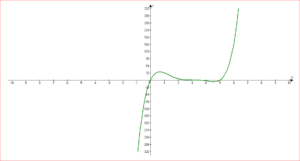
решение: \( x \in (0; 3) \bigcup (5; +\infty) \) -
\( x(x-3)^2 \cdot (x-5) \leq 0 \)
т.к. корень x = 3 имеет кратность 2 (четная), то знак не меняется.
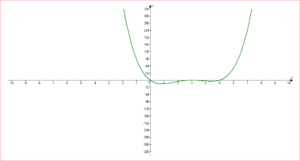
решение: \( x \in [0; 3] \bigcup [3; 5] \) или \( x \in [0; 5] \) -
\( x(x-3)^2 \cdot (x-5) \lt 0 \)
т.к. корень x = 3 имеет кратность 2 (четная), то знак не меняется.
решение: \( x \in (0; 3) \bigcup (3; 5) \)
-
\( x(x-3)^3 \cdot (x-5) \gt 0 \)
-
В разложение многочлена входит квадратный трёхчлен, который не имеет действительных корней, а значит, не раскладывается на линейные множители.
В этом случае он нигде не обращается в нуль и не меняет знак, следовательно, его можно отбросить, если этот трёхчлен принимает только положительные значения.
Если же квадратный трёхчлен принимает только отрицательные значения, то его тоже можно отбросить, но при этом поменять знак неравенства на противоположный.Пример
\( (x+3) \cdot (x^2 + 3x + 10) \gt 0 \)
Т.к. трехчлен не имеет действительных корней \( (D \lt 0) \) и коэффициент при \(x^2\) положителен,
то этот трёхчлен принимает положительные значения для всех \( x \),
т.е. решение исходного неравенства равносильно решению неравенства \( x+3 \gt 0 \).
Откуда \( x \gt -3 \). -
Пусть надо решить неравенство вида:
\( \frac{P(x)}{Q(x)} \gt 0 \;\; (\lt, \; \geq, \; \leq) \)
где \( P(x) \) и \( Q(x) \) — многочлены, которые можно разложить на множители.Поскольку на знак выражения не влияет, находится ли множитель в числителе или в знаменателе,
то это неравенство можно заменить неравенством \(P(x) \cdot Q(x)\gt 0\),
т.е. решение свести к первому случаю, но при этом обязательно исключить точки, в которых \(Q(x)=0\).
Если неравенство не строгое, то значения \( x \), при которых \(Q(x)=0\),
могут войти в множество решений неравенства \(P(x) \cdot Q(x)\geq 0\);
в этом случае их необходимо исключить из ответа, т.к. они не входят в ОДЗ исходного неравенства.
В случае же строгого неравенства этого можно не опасаться.Пример
$$ \frac{x(x+5)}{(x-3)(x+7)^2}\leq 0 $$
т.к. \( (x+7)^2 \geq 0 \), то исходное неравенство равносильно следующей системе:
$$ \begin{cases} x(x+5)(x-3) \leq 0 \\ x \neq 3 \\ x \neq -7 \end{cases} $$решение выглядит так:
ответ: \(x \in (-\infty; -7) \bigcup (-7;-5) \bigcup [0;3)\). -
Прежде чем применить метод интервалов, необходимо привести линейные множители к виду \(x-a\),
разделив обе части неравенства на коэффициент при \( x \) (в каждой скобке).
многочлены при этом нужно разложить на множители.Пример
$$ (5x+3)(6-2x)(x^2-2x-3) \geq 0 $$
Преобразуем выражение и получим:
$$ (x+\frac{3}{5})(3-x)(x+1)(x-3) \geq 0 $$
Ответ: \(x \in [-1; -3/5] \bigcup [3; 3] \).
