§4.3. Равнобедренный треугольник

Пусть Δ ABC – равнобедренный с основанием AB. Рассмотрим Δ BAC. По первому признаку эти треугольники равны. Действительно, AC = BC; BC = AC; ∠C = ∠C. Отсюда следует ∠A = ∠B как соответствующие углы равных треугольников. Теорема доказана.

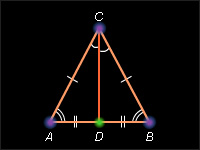
Пусть Δ ABC – равнобедренный с основанием AB, и CD – медиана, проведенная к основанию. В треугольниках CAD и CBD углы CAD и CBD равны, как углы при основании равнобедренного треугольника (по теореме 4.3), стороны AC и BC равны по определению равнобедренного треугольника, стороны AD и BD равны, потому что D – середина отрезка AB. Отсюда получаем, что Δ ACD = Δ BCD.

Из равенства треугольников следует равенство соответствующих углов: ∠ACD = ∠BCD, ∠ADC = ∠BDC. Из первого равенства следует, что CD – биссектриса. Углы ADC и BDC смежные, и в силу второго равенства они прямые, поэтому CD – высота треугольника. Теорема доказана.

Пусть Δ ABC – треугольник, в котором ∠A = ∠B. Δ ABC равен Δ BAC по второму признаку равенства треугольников. Действительно: AB = BA; ∠B = ∠A; ∠A = ∠B. Из равенства треугольников следует равенство соответствующих его сторон: AC = BC. Тогда, по определению, Δ ABC – равнобедренный. Теорема доказана.

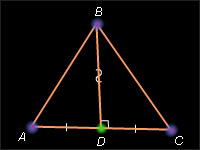
В треугольнике ABC проведем медиану BD, которая по условию также является высотой. Прямоугольные треугольники ABD и CBD равны, т. к. катет BD общий, AD = CD по построению. Следовательно, гипотенузы этих треугольников равны как соответственные элементы равных треугольников, т. е. AB = BC. Теорема доказана.

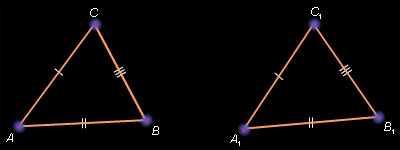
Пусть Δ ABC и Δ A₁B₁C₁ таковы, что AB = A₁B₁; BC = B₁C₁; AC = A₁C₁. Доказательство от противного.

Пусть треугольники не равны. Отсюда следует, что $\angle A\ne \angle A_1;\angle B\ne \angle B_1;\angle C\ne \angle C_1$ одновременно. Иначе треугольники были бы равны по первому признаку.

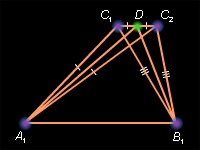
Пусть Δ A₁B₁C₂ – треугольник, равный Δ ABC, у которого вершина C₂ лежит в одной полуплоскости с вершиной C₁ относительно прямой A₁B₁. По предположению вершины C₁ и C₂ не совпадают. Пусть D – середина отрезка C₁C₂. Треугольники A₁C₁C₂ и B₁C₁C₂ – равнобедренные с общим основанием C₁C₂. Поэтому их медианы A₁D и B₁D являются высотами. Значит, прямые A₁D и B₁D перпендикулярны прямой C₁C₂. A₁D и B₁D имеют разные точки A₁ и B₁, следовательно, не совпадают. Но через точку D прямой C₁C₂ можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию. Теорема доказана.

Рис. 4.3.3.

Рис. 4.3.4.