Рассмотрим прямоугольный равнобедренный треугольник с углом при основании, равным \( 45° \). Пусть катеты его равны \( a \). Тогда по теореме Пифагора его гипотенуза будет равна \( \sqrt{a^2 + a^2} \).
Поэтому:
$$ sin 45^\circ = \frac{ \sqrt{2a^2} }{a} = \frac{ \sqrt{2} }{2} $$
$$ cos 45^\circ = \frac{ \sqrt{2a^2} }{a} = \frac{ \sqrt{2} }{2} $$
$$ tg 45^\circ = \frac{a}{a} = 1 $$
Рассмотрим равносторонний треугольник \( ABC \) со стороной, равной \( a \). Проведем в нем медиану \( BD \). Получим треугольник \( ABD \) – прямоугольный с острым углом при вершине \( B \) и стороной \( AD = \frac{a}{2} \).
По теореме Пифагора \( BD = \sqrt{a^2 - \frac{a^2}{4}} = \frac{ a \sqrt{3} }{2} \)
Значит:
$$ sin 30^\circ = cos (90^\circ - 30^\circ) = cos 60^\circ = \frac{a}{2} \div a = \frac{1}{2} $$
$$ sin 60^\circ = cos 30^\circ = \frac{ a \sqrt{3} }{2} \div a = \frac{ \sqrt{3} }{2} $$
$$ tg 30^\circ = \frac{ sin 30^\circ }{ cos 30^\circ } = \frac{1}{2} \div \frac{ \sqrt{3} }{2} = \frac{1}{\sqrt{3}} $$
$$ tg 60^\circ = \frac{ sin 60^\circ }{ cos 60^\circ } = \frac{ \sqrt{3} }{2} \div \frac{1}{2} = \sqrt{3} $$
Составим таблицу известных углов и значений синуса, косинуса и тангенса для них.
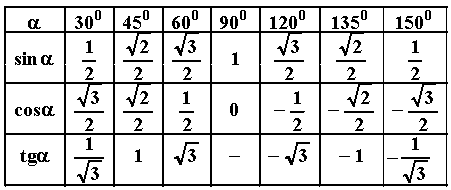
С благодарностью к источнику: Открытая Математика. Планиметрия.
