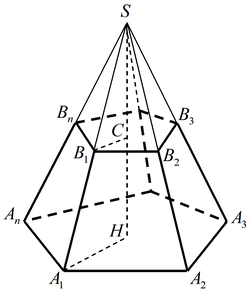
Усеченной пирамидой называется многогранник, у которого вершинами служат вершины основания и вершины ее сечения плоскостью, параллельной основанию.
Свойства усеченной пирамиды:
- Основания усеченной пирамиды — подобные многоугольники.
- Боковые грани усеченной пирамиды — трапеции.
- Боковые ребра правильной усеченной пирамиды равны и одинаково наклонены к основанию пирамиды.
- Боковые грани правильной усеченной пирамиды — равные между собой равнобедренные трапеции и одинаково наклонены к основанию пирамиды.
- Двугранные углы при боковых ребрах правильной усеченной пирамиды равны.
Площадь поверхности и объём усеченной пирамиды
Пусть \( CH \) — высота усеченной пирамиды,
\( P_1 \) и \( P_2 \) — периметры оснований усеченной пирамиды,
\( S_1 \) и \( S_2 \) — площади оснований усеченной пирамиды,
\( S_{бок} \) — площадь боковой поверхности усеченной пирамиды,
\( S_{полн} \) — площадь полной поверхности усеченной пирамиды,
\( V \) — объем усеченной пирамиды.
Тогда имеют место следующие соотношения:
\( S_{полн} = S_1 + S_2 + S_{бок} \)
\( V = \frac{1}{3}CH(S_1 + S_2 + \sqrt {S_1 S_2 }) \).
Если все двугранные углы при основании усеченной пирамиды равны \( \beta \), а высоты всех боковых граней пирамиды равны \( h_{бок} \), то
\( S_{бок} = \frac{1}{2}(P_1 + P_2 )h_{бок} \)
\( S_{бок} = \frac{{|S_1 - S_2 |}}{{\cos \beta }}\;. \)
С благодарностью к источнику: Физ-мат класс. Стереометрия.
