
Определение и численные значения
Золотым сечением (золотой пропорцией, делением в крайнем и среднем отношении, гармоническим делением) называется соотношение величин \( a \) и \( b \) \( (a > b) \), когда справедливо равенство (Рис. 1): $$ \frac{a + b}{a} = \frac{a}{b} $$
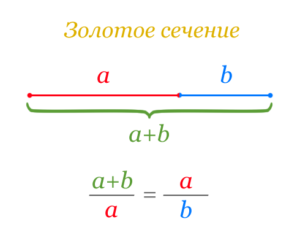
Число, равное соотношению \( \frac{a}{b} \) обычно обозначают прописной греческой буквой \( Ф \) (в честь древнегреческого скульптора и архитектора Фидия).
Из исходного равенства можно получить, что: $$ Ф = \frac{ \sqrt{5} + 1 }{2} \approx 1,618 $$

Для практических целей обычно используют значение \( Ф = 1,62 \) .
Величину \( \frac{1}{Ф} = \frac{ \sqrt{5} - 1 }{2} \approx 0,618 \) обозначают строчной греческой буквой \( \varphi \).
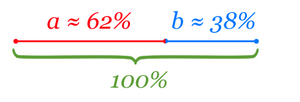
Если взять общую длину отрезка \( (a + b) \) за 100%,
то длина отрезка a будет составлять 62% (округленное значение),
а длина отрезка b – 38% (округленное значение). (Рис. 2)
Геометрическое построение
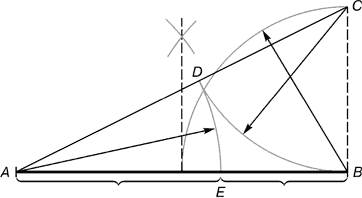
На отрезке AB построим точку E, которая делит отрезок AB так, что AB / AE = Ф
- Из точки B проведем перпендикуляр к отрезку AB.
- Да данном перпендикуляре отложим отрезок BC, равный половине отрезка AB.
- Соединим точки C и A.
- На отрезке CA отложим отрезок CD, равный отрезку CB.
- На отрезке AB отложим отрезок AE, равный отрезку AD.
Докажем, что точка E – искомая.
Поскольку при любых длинах начального отрезка AB соотношение AB / AE будет сохранятся в силу подобия – для простоты расчетов будем считать отрезок AB равным единице.couponsmy companybuy
Пусть AB = 1
Так как треугольник ABC – прямоугольный, то:
\( AC^2 = AB^2 + BC^2 \)
Так как BC – половина AB, то:
\( AC^2 = (2 \cdot BC)^2 + BC^2 \)
\( AC^2 = 5 \cdot BC^2 \)
\( AC = \sqrt{5} \cdot BC \)
Поскольку \( BC = 1/2 \), то
\( AC = \frac{ \sqrt{5} }{ 2 } \)
Так как \( AD = AC – CD \) и \( CD = 1/2 \) , то:
\( AD = \frac{ \sqrt 5 }{2} - \frac{1}{2} = \frac{\sqrt 5 - 1}{2} \)
Так как \( AD = AE \), то:
\( AE = \frac{\sqrt 5 - 1}{2} \)
Теперь определим значение соотношения \( AB / AE \) :
\( \frac{AB}{AE} = 1 \div \frac{\sqrt 5 - 1}{2} = \frac{2}{\sqrt 5 - 1} = \)
\( = \frac{ 2 \cdot (\sqrt 5 + 1) }{ {\sqrt 5 - 1} \cdot (\sqrt 5 + 1) } =
\frac{ 2 \cdot (\sqrt 5 + 1) }{ 5 - 1 } = \frac{ \sqrt 5 + 1 }{2} = Ф \)
Что и требовалось доказать,
\( \frac{AB}{AE} = Ф \)
Следовательно, точка E – искомая.
Алгебраические свойства
-
\( Ф \) – иррациональное алгебраическое число.
Является положительным решением квадратного уравнения:
\( x^2 - x - 1 = 0 \)
Отсюда следуют соотношения:
\( Ф^2 - Ф = 1 \)
\( Ф \cdot (Ф - 1) = 1 \) -
Число \( Ф \) также можно выразить через тригонометрические функции:
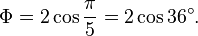
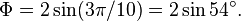
- \( Ф \) представляется в виде бесконечной цепочки квадратных корней:
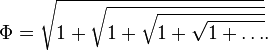
- \( Ф \) представляется в виде бесконечной цепной дроби:
подходящими дробями которой служат отношения последовательных чисел Фибоначчи.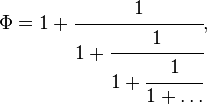 Таким образом,
Таким образом,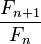 Значения дроби после запятой для \( Ф, \frac{1}{Ф}, Ф^2 \), в любой системе счисления будут равны
Значения дроби после запятой для \( Ф, \frac{1}{Ф}, Ф^2 \), в любой системе счисления будут равны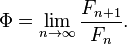
Геометрические свойства
-
Если отрезать квадрат от прямоугольника, построенного по принципу золотого сечения, то получим новый прямоугольник с тем же соотношением сторон, что и у первоначального.
$$ Ф = \frac{a + b}{a} = \frac{a}{b} $$
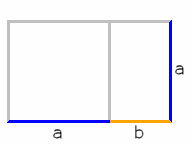
-
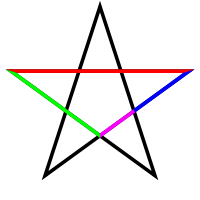
В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении. На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны \( Ф \). Кроме того, отношение красного отрезка к расстоянию между соседними вершинами звезды, которое равно зелёному отрезку, также равно \( Ф \).
- Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
Золотое сечение в архитектуре
Мексика


Мексиканские пирамиды построены с использованием пропорций золотого сечения.
Hа попеpечном сечении пиpамиды видна фоpма, подобная лестнице. В пеpвом яpусе 16 ступеней, во втоpом 42 ступени и в тpетьем - 68 ступеней.
Эти числа основаны на соотношении Фибоначчи следующим обpазом:
16 x 1.618 = 26
16 + 26 = 42
26 x 1.618 = 42
42 + 26 = 68Египет
Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона говорят о том, что египетские мастера пользовались соотношениями золотого деления при их создании.
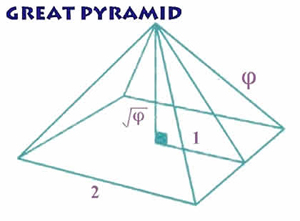


Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления.
Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.
Древняя Греция
Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада.

При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира.
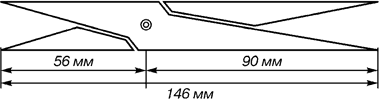
Античный циркуль золотого сеченияКитай
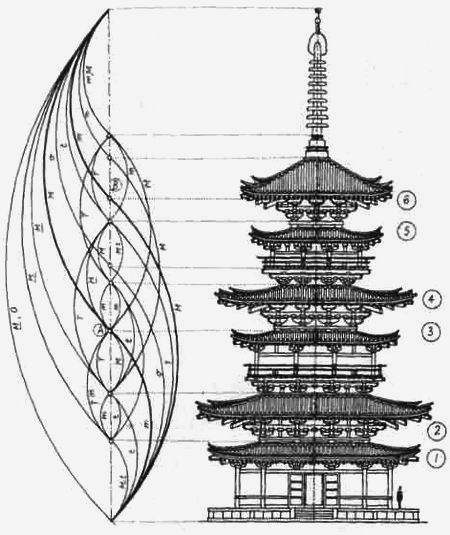
Китайский храм. Их очень много в Китае, и построены они в самое разное время.
Россия

Храм Василия Блаженного. Расположен в Москве на Красной площади. Построен в 1561 году.
Золотое сечение в искусстве

Рождение Венеры. Написана картина в 1486 году известным итальянским художником Сандро Батичелли.

Боярыня Морозова. Создана в 1887 году русским художником В.И. Суриковым. На данный момент выставлена в Третьяковской галерее.
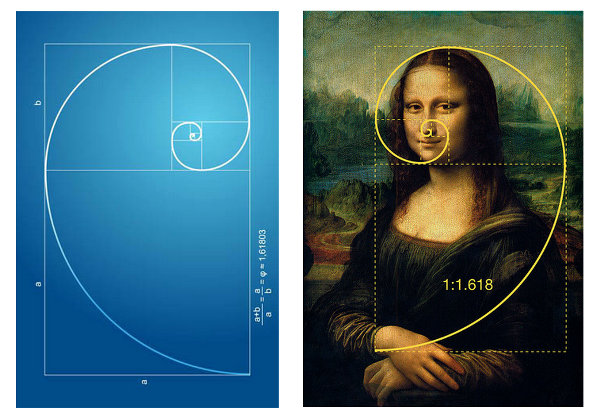
Мона Лиза. Одна из самых известных в мире картин. Написана в 1519 году Леонардо да Винчи.
Золотое сечение в природе
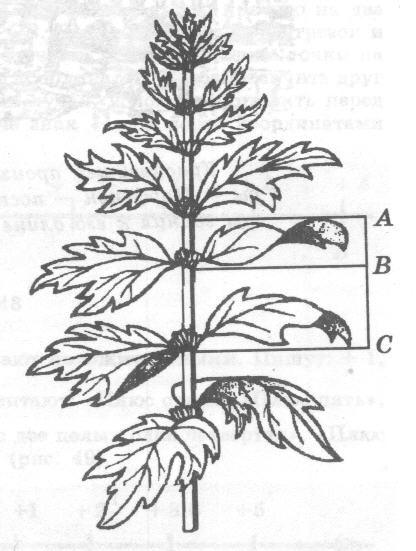
Растение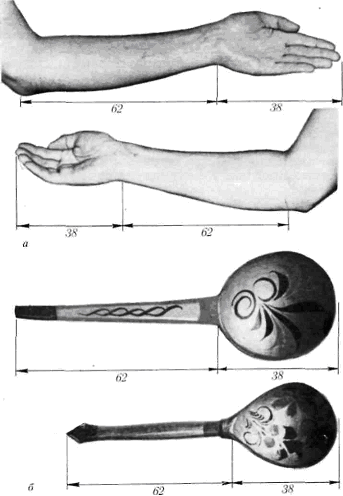
Рука человека, ложка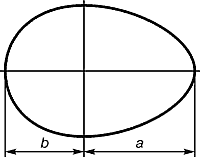
Яйцо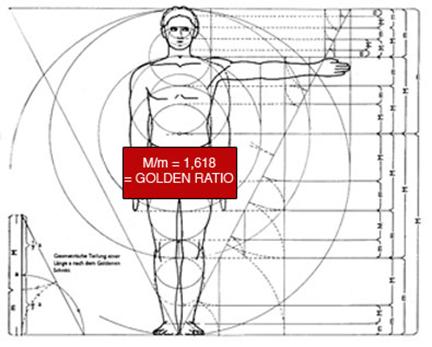
Человек в полный рост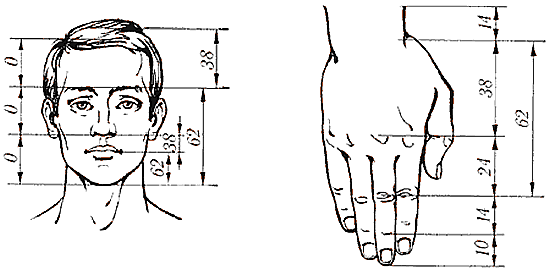
Пропорции человека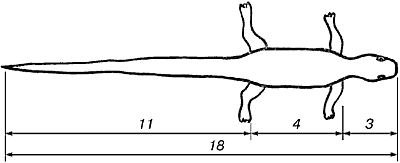
Ящерица - \( Ф \) представляется в виде бесконечной цепочки квадратных корней:
