The post Многомерные числа или Ноль — имеет значение, а Бесконечность — конечна! first appeared on Математику в помощь.
]]>Аннотация: В статье описан принципиально новый метод представления чисел, с помощью которого возможно решить проблему потери данных при умножении на ноль и получения неопределённости при делении на ноль.
Ключевые слова: деление на ноль; оперирование бесконечностью; многомерные числа
Введение
Исторически «ноль» является проблемой в математике: с одной стороны, без ноля невозможно представить современную математику, с другой использование ноля накладывает некоторые ограничения в расчётах (например, деление на ноль).
Актуальность
В большинстве случаев математики и программисты смирились с неудобствами в расчётах, связанных с нолём, получение неопределённости при делении на ноль и потеря данных при умножении на ноль.
Новый метод представления чисел может дать возможность «не смирившимся» делить и умножать на ноль и бесконечность бесконечно много раз и при этом не «терять» результат расчётов.
Научная новизна
Предлагаемое принципиально новое понимание ноля и бесконечности, может раскрыть, для научного мира множество парадоксов и решить до сего момента не решённые задачи.
История ноля и его представление в современной математике
Понятие ноля и бесконечности в истории отлично описана Чарльзом Сейфе [1].
Современное понимание ноля и бесконечности:
Ноль - это «портал» в другие миры
Те, кто из нас помнят начальную школу могут сказать, что там нас учили, что 0 — это пустота или отсутствие чего-либо. Если у Тани 0 яблок, а у Саши 5 яблок, сколько у Тани и Саши яблок?
\( 0 + 5 = 5 ; \)
Нет сомнений, ни у кого не может быть меньше 0 яблок.
Первый портал ноля
Но потом, в средней школе оказалось, что существуют числа меньше ноля.
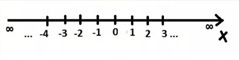
Появление отрицательных чисел стало логическим продолжением оператора вычитания «-», когда из меньшего числа мы вычитаем большее, само появление отрицательных чисел никого не смутило (за малостью лет мы не задали вопрос Марье Ивановне, мол, а как может быть у Тани меньше 0 яблок), и мы приняли это как данность, и пошли дальше.
Второй портал ноля
Вроде всё ясно, числа могут быть положительными и отрицательными (ты можешь быть в прибыли, а можешь получить убыток), и мы все с этим смирились.
Но вот оказалось, что всё не так просто:
Возведение в степень и извлечение корня из отрицательного числа не давали однозначных решений, и тогда появилась гениальная теория мнимых чисел, она всё нам объяснила.
Корень из отрицательного числа может быть как положительным, так и отрицательным (это число назвали мнимым, оно и существует и нет одновременно).
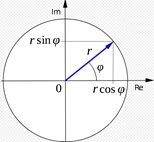
Прекрасно, мнимые числа описаны Марком Беньевичем Балк [2].
Вроде всё понятно, но…
Третий (крайний) портал ноля
Что делать, когда нам приходиться делить на ноль?
Всё что нам объяснили в школе (кроме примера с калькулятором) так-то что при делении на ноль получается «бесконечность».
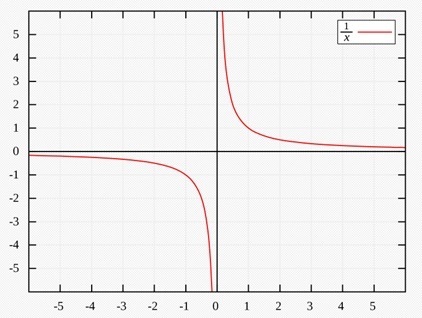
Бесконечность? А что это такое? Это не число! Это то что поглощает любые числа, все числа делятся на все, кроме ноля, поделив на ноль мы получаем «бесконечность», то есть «не число»!
Те, кто учился в институте могут вспомнить ещё вот эту картинку:
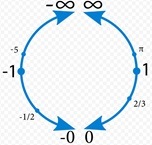
Но нам никто не рассказал, что делать с вот этими выражениями:
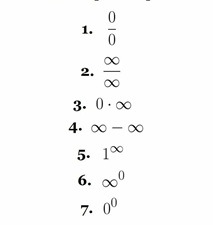
Все эти уравнения не имеют решения.
Те из нас кто глубоко изучал высшую математику ещё вспомнят вот эту картинку:
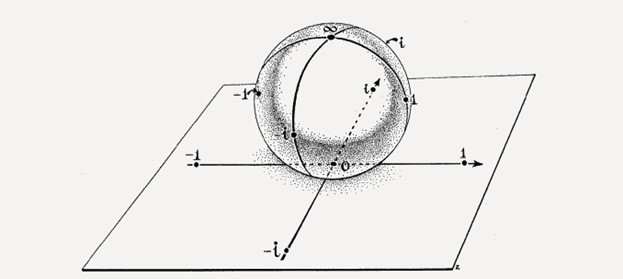
Это сфера Римана.
Которая объясняет нам проблему деления на ноль и что в итоге получается.
Прежде чем перейти к сути, немного поразмышляем:
Давайте на время забудем о том чему нас учили и попробуем ответить, на несколько вопросов про бесконечность, так как вы это понимаете на житейском уровне.
Вопросы о бесконечности:
| Что больше: | \( \infty \) или \( \infty \) ? Очевидно что они равны? Или нет? |
| Что больше: | \( \infty \) или \( \infty + 100 \) ? или они равны? Или нет? |
| А если так: | \( \infty \) или \( \infty + 10000000000000 \) ? |
| А так?: | \( \infty \) или \( \infty * 2 \) ? Так кажется точно второе значение больше? |
| А если так: | \( \infty \) или \( \infty * \infty \) ? Вот тут, то сто процентов правое выражение больше? |
Классическая математика говорит о том, что все эти выражения не имеют ответа, то есть нельзя поставить ни один из знаков неравенства.
Несмотря на то, что ниже приведённые умозаключения противоречат самому понятию "бесконечности" прошу Вас прочесть их и постараться понять.
Если представить что бесконечность имеет какой-то конечный вид, то было бы логичным заключение о том, что две бесконечности больше чем одна. А бесконечно много бесконечностей, тем более больше, чем просто бесконечность.
Оказывается, если поменять представление о бесконечности, то становиться возможным оперировать ею как обычным числом. При этом изящно решить проблемы деления на ноль и потери данных при умножении на ноль. Для того чтобы числа не растворялись в бесконечности необходимо принять постулат, что бесконечность конечна и она есть обратное от абсолютного ноля.
Многомерные числа и их представление
Для начала дадим некоторые определения, выражениям которыми будем пользоваться в дальнейшем:
Классический ноль – это тот самый ноль (в классической математике) при умножении на который любого числа мы получаем классический ноль, а при делении на него получается неопределённость (классическая бесконечность).
Классическая бесконечность – эта та самая бесконечность (неопределённость) в которой растворяются все числа при использовании её в качестве оператора.
Многомерный ноль – это любое число, делённое на бесконечность (многомерную бесконечность) в первом представлении многомерный ноль это $$ \frac{n}{\infty} = n * \infty^{-1} $$ где n - любое (классическое) число не равное классическому нулю или классической бесконечности, например, единица (в дальнейшем первоначальный ноль при автозаполнении баз данных будем представлять именно как $$ 1 * \infty^{-1} $$ . Это выражение не противоречит классической математике, т.к. любое число, делённое на бесконечность это ноль. Для понимания: в общем случае многомерный ноль это $$ n * \infty^{-m} $$ где m – целочисленное число от 1 до \( \infty \).
Многомерная бесконечность – это любое число, умноженное на бесконечность (многомерную бесконечность) в первом представлении многомерная бесконечность это $$ n * \infty^{1} $$ где n - любое (классическое) число не равное классическому нулю или классической бесконечности, например, единица (1). В общем случае многомерная бесконечность это $$ n * \infty^{m} $$ где m – целочисленное число от 1 до \( \infty \).
Число нулевого (существующего) измерения – это классическое число, которое представленное в многомерном выражении как $$ n * \infty^{0} $$
Размерность (измерение) – это целочисленное число, в степь которого возведена бесконечность в представлении многомерных чисел, функции сложения и вычитания возможны только с числами той же размерности (измерения). Размерность может быть отрицательной
И так, в общем случае, действительные числа
$$ 1 * \infty^0 \; , \; 2 * \infty^0 \; , \; 3 * \infty^0 \; , \; $$ и т.д.
Где степень, в которую возведена бесконечность говорит об измерении, в котором находится значение.
То есть, нулевая степень – значит наше обычное (классическое) измерение.
(-1) «минус первая» как и -2, и -3…. и т.д. степень говорит о том, что это значение на одно или несколько измерений ниже классического, и в представлении классической математики это ноль.
Соответственно 1, 2, 3 и т.д. степень говорит нам о том, что значение находится на одно или несколько измерений выше чем классическое и в классическом случае это бесконечность.
Для начальных условий принимаем $$ 0 = 1 * \infty^{-1} $$
Если делим на ноль любое число, то степень бесконечности увеличивается на единицу, если умножаем то уменьшается.
и получаем: $$ \frac{X}{0} = \frac{X}{1 * \infty^{-1}} = X * \infty^{1} $$ то есть обычную в нашем понимании бесконечность, но при этом число не теряется в бесконечности. А остаётся для дальнейших расчётов, и если в последующих расчётах его умножить на «ноль» $$ 1 * \infty^{-1} $$ то степень бесконечности уменьшиться, и число не будет потеряно)
Таким образом, исключается потеря данных при умножении или делении на ноль.
Многомерная арифметика (или сложение и вычитание бесконечностей с обычными числами):
Если обычное число представить как: $$ X * \infty^{0} + X * \infty^{-1} + ... X * \infty^{-n} ... X * \infty^{-\infty} $$ становиться ещё интереснее.
В программировании можно задать бесконечный список, с помощью которого можно описать вышеприведённое число.
Теперь можно вычитать и складывать бесконечность с обыкновенными числами без потери данных
Например:
|
\( 1 * \infty^{1} \) Бесконечность |
+ |
\( 20 * \infty^{0} \) Обычное число |
Машина поймёт, что к числу первого порядка прибавляется число нулевого порядка, и запишет в память, именно так: $$ ( 1 * \infty^{1} ) + ( 20 * \infty^{0} )$$ если в последующем будут прибавляться или вычитаться числа нулевого порядка, то действия сложения или вычитания буду производиться именно с нулевым порядком, то же самое относиться ко всем остальным меньшим порядкам этого числа. В общем случае: складываться или вычитаются числа соответствующих порядков.
Правила умножения и деления в многомерной арифметике такие же как в классической арифметике с умножением и делением многочленов:
результатом умножения одного многомерного числа(Х) на другое(Y), станет такое многомерное число (Z), в котором сложатся произведения каждого измерения числа (Х) с каждым измерением числа (Y) в соответствии с правилами умножения многочленов, например:
|
\( (5 * \infty^{0}) + (20 * \infty^{-1}) \) Это обычное число «5» которому уже довелось складываться с классическим нулём, который в свою очередь уже был умножен на 20 |
* |
\( (2 * \infty^{1}) + (5 * \infty^{0}) \) в обычном понимании это бесконечность, но в многомерной арифметике это две бесконечности, которым довелось суммироваться с обычным числом «5» |
получаем $$ [(5 * \infty^{0}) * (2 * \infty^{1})] + [(20 * \infty^{-1}) * (2 * \infty^{1})] + [(5 * \infty^{0}) * (5 * \infty^{0})] + [(20 * \infty^{-1}) * (5 * \infty^{0})] $$ Или: $$ 10 * \infty^{1} + 65 * \infty^{0} + 100 * \infty^{-1} $$
Деление многомерных чисел:
Деление столбиком) как в многочленах $$ \frac{(10 * \infty^{1}) + (65 * \infty^{0}) + (100 * \infty^{-1})} {(2 * \infty^{1}) + (5 * \infty^{0})} = (5 * \infty^{0}) + (20 * \infty^{-1}) $$
Получаем интересный эффект, если в процессе вычислений мы многократно складываем нули и бесконечности, делим и умножаем, то числовое значение не теряется.
Таким образом, можно число сколь угодно много раз умножить на ноль, а после этого столько же раз разделить на ноль, то мы увидим то самое число.
Реализация в программировании
Прошу прощения за синтаксис, главное понять идею, для примера использован С++.
создаём некий класс или структуру (кому как удобно), например multinumber со следующими членами:
int dimension; // степень бесконечности, по умолчанию для всех чисел кроме ноля степень бесконечности равна 0; для ноля -1.
float value; // собственно само значение числа, может быть отрицательным и положительным,
*multinumber littlenumber // указатель на следующего члена нижнего порядка многомерного числа. На начальном этапе он равен NULL.
Функции:
конструктор по умолчанию, где создаётся объект для классического ноля со следующими значениями
dimension = "-1"; value = "1"; littlenumber = NULL;
конструктор для вводимых данных, где пользователем или программой задаются значения
dimension = "Y"; value = "X"
опять таки если пользователь создаёт ноль то создаём объект по умолчанию.
деструктор в котором не забываем прописать рекуперативное удаление всех младших членов.
Ну и собственно перегружаем арифметические функции для членов этого класса(или структуры):
для "+" и "-" если степень бесконечности равны и нет младших членов то соответственно сумируем или вычитаем значение value и возвращаем с тем же значением dimension, если у слагаемых есть младшие члены то соответственно делаем с ними тоже самое. если dimension не равны, то слагаемому с большим значением степени бесконечности, добавляем littlenumber с указателем на слагаемое с меньшим значением dimension (все числа, кроме ноля по умолчанию $$ 1 * \infty^{-1} $$ , который мы просто игнорируем)
для "*" для старших членов умножаемых multinumber перемножаем value и суммируем dimension, если есть младшие члены то в возвращаемом multinumber добавляем соответствующие littlenumber в соответствии с правилами умножения многочленов.
для "/" для старших членов multinumber соответственно вычитаем dimension и соответственно делим value, если есть младшие члены то в соответствии с правилами деления многочленов делим их.
Можно также прописать функцию отображения значений для пользователя, где у нас три варианта значений
с dimension меньше ноля тогда отображаем "0";
dimension = 0; тогда отображаем value;
и dimension больше ноля тогда отображаем "infinity"
теперь подставляем вместо обычных float наш multinumber и вуа-ля, наслаждаемся делением на ноль)
эта модель работает на всех видах числовых данных, в том числе опробована на комплексных числах.
Честно признаться, младшими членами можно пренебречь и оперировать только старшими. Мне пока не довелось, встретится с задачей, где младшие члены многомерного числа играли роль, хотя допускаю, что такие задачи могут быть.
Если пренебрегать младшими членами то класс(структура) multinumber становится ещё проще.
Библиографический список
1. Чарльз Сейфе. Ноль: биография опасной идеи, 2014
2. Балк М.Б. Реальные применения мнимых чисел, 1988
С благодарностью к источнику: SCI-ARTICLE.RU
The post Многомерные числа или Ноль — имеет значение, а Бесконечность — конечна! first appeared on Математику в помощь.
]]>The post Что спрятано за покровом очевидностей в математике и привычном всем мире first appeared on Математику в помощь.
]]>Выражаю сердечную благодарность Александру Сазонову за глубокие комментарии к этой статье при её создании. Без его работы статья бы не была настолько полной.
В повседневной жизни нас окружает много очевидностей. Мы давно к ним привыкли и уже не рассуждаем: почему? Тем более, нам это не свойственно делать по отношению к тому, о чём мы узнали в глубоком детстве. Всё это воспринимается как само собой разумеющееся.
Хотя, на самом-то деле, всё может быть совсем и не так. И ключики к секретам нашего мира часто бывают скрыты как раз за пеленой многих очевидностей. Надо заметить, что это одно из самых надёжных мест, где можно хранить тайны от входов в другие миры.
В этой статье я как раз хочу убрать покров с одной из очевидностей. С младшей школы, где мы изучали арифметику, нас учили сложению и вычитанию, умножению и делению. И заставляли запомнить, что на ноль делить нельзя. А если умножить число на ноль, то в результате получим ноль. Все мы это прекрасно запомнили, а вот почему именно так — не знаем. Давайте разберёмся в этом вопросе.
Умножение, как учили нас в школе, представляет собой более короткую запись процесса сложения одинаковых чисел несколько раз. Например, если
Далее наблюдаем интересное. Если любое число умножить на ноль, то получим ноль. На самом деле, если взять любое число ноль раз, то либо получим ноль, так как ничего не брали, либо само исходное число, так как к нему ничего не прибавили, точнее, прибавили к нему его же, только ноль раз. (Исходное число всё-таки есть, но мы к нему можем что-нибудь прибавить, а можем и не прибавить вообще ничего, то есть ноль.) На этом этапе у нас уже есть двойственная неопределённость с операцией умножения, в отличие от того, как это правило дают в школе, где подразумевается полная однозначность операции умножения на ноль, когда в итоге любое число станет нулём. Но давайте вернёмся к эквиваленту умножения — к сложению.
Выходит интересный парадокс. Для всех чисел наблюдается взаимнооднозначное преобразование сложения в умножение и наоборот, исключением является только число ноль. В результате он нам может дать либо само исходное число, если мы идём от сложения, либо ноль, если следуем формальной логике умножения. То есть, в случае с нулём сложение не эквивалентно умножению, как при любых других участвующих цифрах.
Теперь рассмотрим деление на ноль. По смыслу деления можно сказать, что это сколько раз ноль находится в каком-то числе. И тут ясно, что ответы могут быть разнообразны. Вопрос в том, как мы понимаем ноль. Это может быть и 1 раз, и несколько, и бесконечность, и ни одного раза. Неопределённость здесь становится по-настоящему безграничной.
Но если мы задаёмся вопросом, сколько будет 12 разделить на ноль? То есть сколько раз ноль содержится в 12, то ответом будет нисколько. Ноля нет. В числе 12 его нет. Значит и ответ этого деления будет ноль. Опять получаем, что сложение не эквивалентно умножению в случае с нолём.
Рассмотрим простые примеры.
Предположим, у нас есть какой-нибудь предмет. Например, книга. Мы можем взять её, например, 5 раз, и получим 5 книг. Эту операцию можно записать и как процесс умножения 1х5. Далее. У нас есть эта же книга. Она есть. Предположим, мы её хотим взять 0 раз. Что можно сказать об этом, что мы получим? Книга как была, так и осталась на месте. Но мы её не взяли. Значит, ответом может быть и ноль, и единица. Посмотрим глубже. Книга как была в пространстве в определённом месте, так и осталась. При этом процесса перемещения, который связан со временем, не произошло. В нашем мире время связано с состояниями изменения, с протеканием каких либо процессов. Напрямую, в чистом виде, оно не присутствует в нашем восприятии мира. То есть, если ноль у нас связан с измерением пространства и мы какой-то объект, пусть даже цифру, умножаем на ноль, связанный с измерением пространства, то мы как бы не даём этому объекту нового пространства. То есть, он остаётся, где и был. Если же мы под нолём понимаем измерение времени, то ноль означает отсутствие времени. При умножении на него у нас из времени пропадает и первоначальный объект, мы как бы не даём ему возможность жить дальше. В этом случае мы получаем в ответе ноль.
Рассмотрим процесс деления. Например, у нас имеется 10 книг. Попробуем их разделить на ноль. По смыслу это — сколько нолей книг содержится в 10 книгах. Итак, если мы под нолём понимаем не бесконечно малое число, а отсутствие всего, то правильный ответ — нисколько, то есть ноль. При этом, при делении на ноль, все книги никуда не исчезают из одной, например, стопки, как было бы, например, при делении на 5, где мы все книги бы могли разложить по 2 в пять стопок. То есть, можно говорить, что ответом в данной задаче является также и число 10. Здесь, говоря о книгах, мы подразумеваем пространственный объем. Мы к этому привыкли и считаем само собой разумеющимся. Но у нас также есть и время. Если мы под нолём понимаем отсутствие времени, то 10 книг при делении на ноль также дадут ноль — полное отсутствие всего. Но уж никак не бесконечность, как нас учили с детства.
Как видно, сама природа ноля является неоднозначной. Давайте подробнее попробуем разобраться в этом.
Если обратиться к истории математики, то видно, что современная математическая теория была создана как многослойная надстройка над разнородными теориями и практическими методами, возникшими в разных цивилизациях и для разных целей. К примеру, изначально числа рассматривались людьми с практической точки зрения — счёт (предметов), позже добавились площади и объёмы, что привело к прямой необходимости введения дробей, однако даже у тех народов, где дроби эффективно использовались, они всё равно не считались настоящими числами. Одной из основных целей введения ноля была необходимость позиционной записи чисел (т.е., когда значение цифры определяется не только самой цифрой, но и её местом — разрядом, пустые разряды заполнялись нулями так, как мы это делаем и сейчас). Ноль не использовался как самостоятельное число и не участвовал в вычислениях. Напротив, отрицательные числа появились как необходимость хранения промежуточных результатов при решении систем линейных уравнений, они имели другое название (обычно эквивалент русскому «долг, задолженность»), не считались «настоящими» числами и не использовались в конечном результате. Подобные же примеры относятся к иррациональным и комплексным числам — они появились из потребностей решать новые более сложные задачи.
Современная теория выглядит гораздо более однородной, чем предшественники. В школах учат как можно раньше переходить от конкретных цифр к абстрактным «x», «y» и т.д. В этом есть очень большой смысл, так как умение работать с разными уровнями абстракции активно развивает интеллект. Но вот здесь и есть один из подводных камней современной математики — мы уже не возвращаемся к основам (к аксиоматике), когда их освоили. Мы больше склонны двигаться вперёд и вверх (если представлять современную теорию, как некое «древо»). Когда нам необходимо расширить теорию на новый класс задач, мы углубляемся дальше в «ветки» и «листья», выращиваем новые «ветви», мы не возвращаемся к «стволу» и «корням» и, таким образом, просто лишены возможности попасть на другие «деревья» и даже представить, что они существуют.
Давайте ещё рассмотрим смысл числа Ноль. Посмотрим, как он представляется и понимается в физике и математике.
Способ применения ноля в математике в значительной степени зависит от того раздела математики, к которому относится рассматриваемая задача. Например, в арифметике ноль — «чистый» ноль, в теории пределов — бесконечно малая величина, в интегральном исчислении — и то и другое.
В физике ноль может быть и бесконечно малой величиной, и «чистым» нулём (что имеет место, например, в физике элементарных частиц: заряд нейтрона равен нулю, а не бесконечно мал, также нулём может быть спин, магнитный момент и другие квантовые числа). Характерной особенностью физики является размерность величин. В физике ноль — это всегда ноль чего-то (метров, секунд, кулонов, граммов и производных величин). Т.е. физический ноль несёт в себе определённую нагрузку в виде размерности. В физике недопустимо использовать нули разной размерности в операциях сложения, вычитания и приравнивания, а в математике с этим нет никаких проблем. Даже формально безразмерные величины разной природы (например, концентрация растворов и фаза волны) недопустимо приравнивать. Деление и в физике является примером очередной неоднозначности: если отношение двух (неизвестных) величин равно нулю, то мы пользуемся чисто математическим подходом — делитель не равен нулю, делимое равно нулю. Этот подход не принимает во внимание ни размерность, ни физические свойства, ни предысторию участвующих в отношении величин (а для физики всё это — значимые вещи).
Введение эквивалентов «сложение – умножение» и «вычитание – деление» относится уже в большей степени к современному этапу развития теории, однако не даёт ответа на следующие вопросы: «как применять принцип эквивалентности, если среди чисел, участвующих в операции, есть ноль или иррациональные». Иррациональное число — бесконечная непериодическая дробь (в любой системе счисления), поэтому мы, даже в теории, не знаем «полную» запись числа, и прямое применение принципа эквивалентности даст алгоритм с бесконечным числом шагов. Тем не менее, при решении уравнений даже в школе нет никаких проблем умножить что-то на «пи» или «корень из двух» и до конца вычислений использовать формульную запись числа, не приводя его к однородному виду (например, к десятичной записи).
Вот здесь и всплывает тот факт, что ноль не создавался как полноценное число, а лишь, как заменитель пустых разрядов. Ноль признали равноправным с остальными числами, когда начали создавать современные классификации (натуральные числа, целые, действительные и т.д.), однако, к этому моменту теория арифметических действий над числами уже была вполне проработана.
Таким образом, современная математическая теория в определённом смысле представляет из себя «лоскутное одеяло», собранное из различных представлений разных народов и эпох, использовавших вычисления для своих целей и нужд. И часто смысл, который вкладывался в понятие «ноль» было другим, чем тот, который мы придаём ему сейчас.
В современном понимании ноль, прежде всего, точка перехода. Переход может быть и между пространствами миров, и между множествами чисел, и ещё много между чем и чем. А в сам момент перехода можно говорить о полной неопределённости.
Что особенно интересное, что в этих точках перехода пропадает полное соответствие процессов сложения и умножения, а также вычитания и деления. А это говорит о том, что существующая сегодня математика не полностью верна. И все теории, доказанные ранее математически, если они касаются любых процессов перехода через ноль — не всегда верны. Стоит учитывать, что все теории, связанные с микромиром и космологией, связанны с нулевыми переходами. Поэтому можно утверждать, что представления о реальности на современном этапе развития человечества далеко не всегда соответствуют действительности и требуют глобального пересмотра.
Ноокосмология как наука работает не только с видимым нами миром, который мы можем воспринимать с помощью физических органов чувств и приборов, являющихся их своеобразным продолжением. Она работает и с невидимым миром. Невидимый мир мы не можем воспринимать напрямую, но знаем о нём по духовному опыту и/или косвенно.
Например. В христианстве говорится об этом свете и о том, что души умерших людей отправляются на тот свет. То есть, есть этот свет и тот свет, недоступный нашему обычному человеческому восприятию. При этом, тот свет представляет собой также целостный мир со своей жизнью и особым укладом её.
Также интересным примером является время. Мы измеряем его всегда по скорости каких-либо процессов, то есть косвенно. Напрямую мы время измерить не можем. Мы не можем его хранить, чтобы пользоваться им как ресурсом. При этом мы его ощущаем, понимаем, что это реальность, и она оказывает на нас воздействие и влияние. Но, в большинстве случаев, мы с этим ничего не можем поделать.
Любопытно, что в книге Р. Бартини «Сборник статей по физике и философии» рассматривает наш мир, как состоящий из 3-мерного пространства и ортогонального к нему 3-мерного протяжённого времени. А существование объекта в нашем мире он описывает (3+3)- мерным комплексным образованием, которое можно рассматривать как состоящим из произведения трёхмерной пространственной и ортогональной к нему трехмерной времяподобной протяжённости, имеющих ориентацию. И доказывает это утверждение.
Также он в этой книге описывает, что различные объекты могут переходить из нашего 3-мерного пространственного измерения в 3-мерное временное измерение, становясь невидимыми в пространственном. Ясно, что при таком описания мира ноль является точкой перехода между мирами. Или, хотя бы переходом от пространственной к временной координате.
Интересно, что если мы построим математический график перехода между двумя мирами, то в точке перехода график будет выглядеть также обычно, как до и после неё. А мы увидим исчезновение какого либо предмета из нашего мира. Возможно, позже и неожиданное появление его. А график будет ровным, без особенностей.
На этом примере можно наглядно видеть, что между теорией и наблюдаемой нами реальностью имеется несоответствие. Как минимум, можно говорить, что наше восприятие мира очень ограничено в таких критических точках перехода. При этом объекты при переходе через ноль не перестают существовать, а продолжают быть. Только мы их уже не можем воспринять обычным путём. И математика наш процесс восприятия действительности, нашу ограниченность ещё адекватно своими теориями не описывает. Также как и не может адекватно описать те миры, которые пока недоступны нашему восприятию.
Не следует думать, что другие миры являются чем-то нереальным. Просто обычный человек их не воспринимает. Например, целителям, работающим с энергетикой, известно, что если убрать из поля патогенную энергию (а лучше и причину на тонких уровнях), связанную с конкретным физическим проявлением болезни, например, опухоли, то болезнь исчезает, человек выздоравливает. Точно также при обратном варианте, то есть традиционном методе лечения, когда воздействие оказывается на физическое проявление болезни, например, вырезается опухоль — исчезает патогенная энергия в поле человека. Одно связано с другим, воздействует друг на друга и взаимоперетекает. Это всего лишь один из примеров, что восприятие мира обычного человека сильно усечено. При этом, другой мир может быть совсем рядом, а не где-то далеко.
Ещё такой момент. Во всех теориях, связанных с пространством, человечество очень долго пользовалось идеей плоских или неплоских изотропных пространств с целочисленной размерностью (евклидова и неевклидова геометрия). Геометрия искривлённых пространств (неевклидова) хотя и имеет отличия даже в аксиоматике (например, аксиомы о параллельных) во многом всё равно заимствует основные идеи «плоской» геометрии. И, в принципе, на этом базисе основана вся современная физическая теория. Вопросы, связанные с различными анизотропными искривлёнными пространствами, пространствами, где искривление зависит от масштаба, т.е. на разных масштабах (микро-, «человеческом» и астрономическом) искривление пространства имеет или разные величины или, даже, разный характер, пространствами с нецелочисленной размерностью — эти вопросы, хотя и поднимались учёными, на практике всё же не используются. И здесь очень существенную роль играют шаблоны, заложенные в детстве, прежде всего, в школе. Исследователь, желающий проникнуть в тайны анизотропных пространств или пространств нецелой размерности, всё равно не хочет отходить от школьных аксиом и правил, предпочитает наращивать новую теорию на готовом субстрате, нежели перейти в другое поле знаний.
ВЫВОДЫ
Главным выводом этой статьи является то, что за пеленой привычных очевидностей мы часто не замечаем реального, живого мира во всём его разнообразии. Очень трудно, когда считаешь что-то незыблемым и само собой разумеющимся, увидеть, что далеко не всё так просто и однозначно, как к этому мы все привыкли с детства. Но если не снимать с себя постоянно пелену очевидностей, которая захватывает наше сознание, восприятие мира в свой плен, то можно ходить зашоренным всю жизнь и так и не узнать, что настоящий мир совсем иной, он далеко не ограничивается тем миром, который описывали нам в школе. И если не снимать постоянно с себя завес очевидностей, то к более широкому, всеобъемлющему восприятию мира никогда не прорваться. Но путь этот очень непрост и требует постоянных усилий, чтобы не скатиться в привычные шаблонные восприятия мира, ограничивающие наше знание.
Современная математическая теория нецельна и содержит в себе немало неточностей и ошибок. В силу этого, наши представления о мире очень ограничены и, что касается особенно микро- и макромира, не очень верны. Связано это, прежде всего, с тем, что нет полного соответствия процессов умножения и сложения, а также деления и вычитания при переходе через ноль. Есть также и другие неточные, неоднозначные или ошибочные места в математике, которые в данной статье не рассматривались.
Если человечество хочет не замыкаться в своём восприятии только на этом, известным всем нам мире, а хочет познакомиться и с существующими другими мирами, то необходима совместная работа всего мирового научного сообщества над пересмотром существующей научной парадигмы.
Невозможно познать целое, подвергая его анализу, то есть, расчленяя на части, стараясь понять, как оно работает. А потом, собирая эти части, получить снова цельную работающую систему. Необходимо разрабатывать и развивать другие методы познания.
15 ноября 2013 года.
С благодарностью к источнику: Ноокосмология
The post Что спрятано за покровом очевидностей в математике и привычном всем мире first appeared on Математику в помощь.
]]>The post Фракталы first appeared on Математику в помощь.
]]>В этой статье приведены примеры расчета и построения графической интерпретации некоторых алгебраических и геометрических фракталов.
Фрактал – сложная геометрическая фигура, обладающая свойством самоподобия, т.е. из всей фигуры можно выделить части, подобные целой фигуре. Примеры самоподобных множеств известны с XIX века. Термин «фрактал» (от лат. fractus - раздробленный) впервые ввел в 1975 году математик исследовательского центра IBM Бенуа Мандельброт.
Фракталы можно разделить на несколько видов:
- Геометрические фракталы – строятся на основе исходной фигуры (линии, многоугольника или многогранника) путем ее дробления и выполнения различных преобразований полученных фрагментов.
- Алгебраические фракталы – строятся на основе алгебраических формул.
- Стохастические фракталы – получаются, если в итерационном процессе случайным образом изменять какие-либо параметры.
Фракталы нашли применение в физике (моделирование сложных процессов и материалов), биологии (моделирование популяций, описание сложных ветвящихся структур), технике (фрактальные антенны), экономике. Существуют алгоритмы сжатия изображений с помощью фракталов. В компьютерной графике фракталы используются для построения изображений природных объектов – растений, ландшафтов, поверхности морей и т. д.burga phone casesee postverified site
Некоторые примеры алгебраических и геометрических фракталов
Фрактал Мандельброта
Рассмотрим последовательность комплексных чисел:
$$ z_{k+1} = z_k^2 + c, k = 0, 1, 2, \dots, z_0 = c $$Множество точек c, для которого эта последовательность не расходится, называется множеством Мандельброта. Для построения его графической интерпретации нужно определить исходные данные:
- прямоугольное окно C с разрешением \( m \times n \) точек;
- значение \( r_{min} = 2 \) – минимальный радиус расходимости множества Мандельброта
- максимальное число итераций \( k_{max} \)
Если точка \( z_k \) вышла за пределы круга радиуса \( r_{min} \) при \( k \lt k_{max} \), то процесс вычисления останавливается.
Построение: для каждой точки \( c_{ij} \in C (i = \overline{1, n}, j = \overline{1, m}, c_x \in [-2; 1], c_y \in [-2; 1,5]) \) запустим итерационный процесс:
$$ x_{k+1} = x_k^2 - y_k^2 + c_x, x_0 = c_x $$ $$ y_{k+1} = 2 x_k y_k + c_y, y_0 = c_y $$где \( k = 0, 1, 2, \dots, k_{max} \) и \( \sqrt{x_k^2 + y_k^2} \leqslant r_{min} \).
Составим матрицу M , элементы которой \( m_{ij} \in [1; k_{max}] \) равны номерам итераций, на которых процесс был остановлен. Далее матрицу можно вывести на экран как растровое изображение, предварительно сопоставив каждому числу из интервала \( [1, k_{max}] \) некоторый цвет.

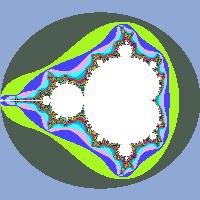
Если представить множество в общем виде:
$$ z_{k+1} = z_k^N + c $$то, изменяя значение N, можно получать симметричные фрактальные множества. Например, для \( N = 4 \) и \( N = 7 \):


Фрактал Жюлиа
Рассмотрим ту же последовательность комплексных чисел, что и для множества Мандельброта:
$$ z_{k+1} = z_k^2 + c, k = 0, 1, 2, \dots $$Исходные данные, этапы построения и условия остановки – те же, что и для фрактала Мандельброта, за исключением:
- значение c фиксируется: \( c = 0,36 + 0,36i \)
- начальное значение \( z_0 \) перебирается дискретно в области \( C \in [-1;1] + [-1;1]i \)

Рассматривая множество в общем виде: \( z_{k+1} = z_k^N + c \) и изменяя N и с, можно получать разнообразные фрактальные множества:
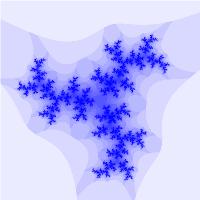
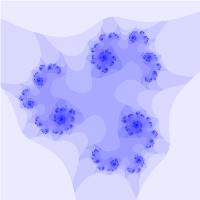

Бассейны Ньютона
Области с фрактальными границами появляются при приближенном нахождении корней нелинейного уравнения алгоритмом Ньютона на комплексной плоскости.
Рассмотрим уравнение:
$$ p(z) = z^3 - 1 $$Общая формула метода Ньютона имеет вид:
$$ z_{k+1} = z_k - \frac{f(z_k)}{f'(z_k)} $$При выборе различных \( z_0 \) процесс будет сходиться к различным корням (областям притяжения). Границы этих областей имеют фрактальную структуру.
Подставив \( p(z) \) в формулу метода, получим итерационную формулу для построения фрактала:
$$ z_{k+1} = z_k - \frac{z_k^3 - 1}{3z_k^2} $$Итерационный процесс останавливается при:
$$ \left| z_{k+1}^3 \right| \leqslant r_{min} $$Для построения графической интерпретации также как и для фрактала Мандельброта, используется матрица, элементы которой равны номеру итерации, на которой остановился процесс.

Если записать формулу в общем виде:
$$ p(z) = z^N - 1 $$ $$ \left| z_{k+1}^N - 1 \right| \leqslant r_{min} $$то можно получить изображения фракталов более сложной формы:



L-системы
В 1968 году венгерский биолог Аристид Линденмайер предложил математическую модель для изучения развития простых многоклеточных организмов, которая позже была расширена для моделирования сложных ветвящихся структур (разнообразных растений). Эта модель получила название Lindenmayer System (Система Линденмайера или L-система).
Рекурсивная природа L-систем позволяет строить с их помощью геометрические фрактальные изображения.
L-система определяется как \( G = (V, \omega, P) \) , где
- V - алфавит – множество символов, содержащее элементы, которые могут быть замещены (переменные).
- ω – строка символов из множества V, определяющая начальное состояние системы (аксиома).
- P – набор правил, определяющий, как переменные могут быть замещены другими переменными и константами.
Правила применяются итеративно, начиная с аксиомы. За одну итерацию применяются одновременно все правила.
Например, L-система имеет вид:
Переменные: A B
Аксиома: A
Правила: \( (A \rightarrow AB) (B \rightarrow BA) \)
После нескольких применений правил из аксиомы получаются строки:
0) A
1) AB
2) ABBA
3) ABBABAAB
4) ABBABAABBAABABBA
…
Для построения графической интерпретации L-системы используется «черепашья графика», т.е. символам из V присваиваются команды управления некоторым простым интерпретатором («пройти вперед», «повернуться», и т. д.).
Пример некоторых фракталов, построенных с помощью L-систем - кривая дракона и растение:


Лист папоротника
Существует несколько способов построения этого фрактала.
1) Построение с помощью системы итерируемых функций (IFS)
Производится 20 итераций функции \( f(x, y) \). Каждое новое значение получается из предыдущего в зависимости от случайного числа, т. е. вычисляется с использованием таблицы распределения:
| Вероятность | $$x'$$ | $$y'$$ |
|---|---|---|
| 0,01 | $$0$$ | $$0,16y$$ |
| 0,85 | $$0,85x + 0,04y$$ | $$-0,04x + 0,85y + 1,6$$ |
| 0,07 | $$0,20x - 0,26y$$ | $$0,23x + 0,22y + 1,6$$ |
| 0,07 | $$-0,15x + 0,28y$$ | $$0,26x + 0,24y + 0,44$$ |
После выполнения всех итераций точка рисуется на экране.
Начальные значения x и y могут быть константами (желательно не большими, чем 1) или их можно выбирать случайным образом на отрезке \( [0;1] \).

2) Рекурсивное построение
Для построения используется процедура (псевдокод):
procedure fern(p0,h,ψ,side,δ,rec){
if (rec=0) or (k2*h< δ) then exit;
p1=p0+[0,k1*h]*R(ψ)
p2=p0+[0,k2*h]*R(ψ)
line(p0,p2) /* процедура построения отрезка по двум точкам */
fern(p1,m1*h,ψ-side*(φ1+φ0),-side,δ,rec-1)
fern(p2,m2*h,ψ+side*(φ2+φ0),side,δ,rec-1)
fern(p2,m3*h,ψ-side*(φ3-φ0),side,δ,rec-1)
}\( R(\phi) = \begin{pmatrix} \cos(\phi) && \sin(\phi) \\ -\sin(\phi) && \cos(\phi) \end{pmatrix} \) - матрица поворота на угол φ.
Параметры процедуры:
- \( p_0 = [x_0; y_0] \) - координаты начальной точки
- h – высота листа
- ψ – угол отклонения листа от вертикали
- side – направление изгиба ветви
- δ – минимальная длина ветви ветвящегося отрезка
- rec – максимальная глубина рекурсии
Рекомендуемые значения углов и коэффициентов: \( \phi_0 = 14,9^{\circ}, \phi_1 = 37,7^{\circ}, \phi_2 = 36,8^{\circ}, \phi_3 = 17,6^{\circ}, k_1 = 0,0483, k_2 = 0,162, m_1 = 0,371, m_2 = 0,336, m_3 = 0,849 \).

Для получения более реалистичного изображения можно использовать метод управляемой случайности. Метод заключается в том, что в процесс сознательно вносятся помехи. В алгоритме построения ветви папоротника можно внести изменения в углы ветвления φ1, φ2, φ3.
Например, если ввести случайные воздействия на углы помех, равномерно распределенных на интервале \( (-10^{\circ}; 10^{\circ}) \), можно получить изображения:
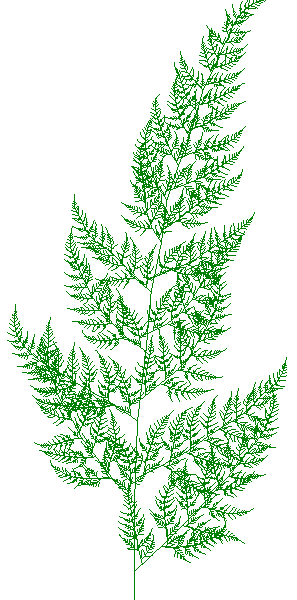

Литература:
- Никулин Е. А. Компьютерная геометрия и алгоритмы машинной графики. – СПб.: БХВ-Петербург, 2005
- “L-System”:http://en.wikipedia.org/wiki/L-system
- “Фрактал”:http://ru.wikipedia.org/wiki/Фрактал
- “Лист папоротника”:http://algolist.manual.ru/graphics/fern.php
- “Синтез фракталов: IFS и L-системы”:http://habrahabr.ru/post/134616/
- “L-Systems — математическая красота растений”:http://habrahabr.ru/post/69989/
- “FRACTALS – построение геометрических фракталов”:http://flash.xaoc.ru/index.swf
- Фракталы - “http://elementy.ru/posters/fractals”:http://elementy.ru/posters/fractals
Программы
Здесь приведены ссылки на программы, с помощью которых были созданы иллюстрации для этой статьи.
Для запуска всех программ нужен .net Framework версии 3.5 или выше.
- “Все файлы на Github”
- “Фрактал Мандельброта”
- “Фрактал Жюлиа”
- “Бассейны Ньютона”
- “L-системы”
- “Лист папоротника”
- “Исходные коды программ” (C#, лицензия BSD)
С благодарностью к источнику: Code More! Фракталы
The post Фракталы first appeared on Математику в помощь.
]]>The post Некоторые общие принципы управления большими системами first appeared on Математику в помощь.
]]>Мы уже говорили о том, что одна из существенных черт биологических систем - это их сложность. Рассмотрим ту живую систему, с которой мы никогда не расстаемся,- наше собственное тело. Если мы, максимально упростив реальную ситуацию, будем рассматривать человеческое тело просто как механическую систему с соответствующим числом шарниров (суставов), то окажется, что эта система имеет более ста степеней свободы. Мы успешно справляемся с задачей управления такой системой: ходим, бегаем, выполняем различные другие движения. В то же время в технических задачах управления приходится, как правило, распоряжаться не более, чем 2-3 параметрами. В теории регулирования разработаны методы, позволяющие успешно решать задачи, связанные с управлением такими относительно несложными системами. Однако эти методы становятся совершенно неэффективными, если мы переходим к системам с десятками и сотнями степеней свободы.
Следует обратить внимание на то, что при решении таких задач, как задача управления движениями нашего тела, весьма важен фактор времени. Если нам нужно избежать какой-либо опасности, скажем, отскочить от движущегося от нас автомобиля, то эту задачу (требующую участия десятков мышц, т. е. достаточно сложную) нужно не просто решить, но решить быстро. Другое соображение, опять же связанное с учетом времени, таково: количество различных положений (поз), которые может принять наше тело, настолько велико, что «перепробовать» все возможные для нас позы мы не смогли бы и за всю жизнь. Поэтому обучаться нужным для нас движениям (например, ходьбе) заведомо невозможно путем последовательного перебора всех возможных движений вообще. Следовательно, живые системы решают задачи построения движений и выработки новых их сочетаний какими-то собственными, весьма эффективными способами, Что же мы знаем по этому поводу?
Синергии
В физиологии движения хорошо известно наличие у организма так называемых «синергий», т. е. четко выраженной координации различных частей тела при тех или иных движениях. Мы не можем, даже если будем стараться, управлять теми степенями свободы, которые имеет наше тело, независимо. Например, для человека весьма затруднительно одновременно выполнять двумя руками вращательные движения так, чтобы одна рука совершала вращения с одной частотой, а другая с другой. Таким образом, при выполнении тех или иных движений происходит распадение имеющихся в нашем теле степеней свободы на согласованно управляемые «блоки». Тем самым реальное число независимых параметров, подлежащих регулированию, оказывается во много раз меньше, чем число степеней свободы, определяемое подвижностью суставов. Некоторые из этих «блоков» в нашем организме твердо зафиксированы, например, согласованность в движениях рук, о которой упоминалось выше,- это не результат обучения или привычки, а врожденное свойство. В других случаях, скажем, при выполнении таких действий, как катание на коньках и т. п., синергии являются следствием соответствующей тренировки.
Интересным примером синергии (природной, а не выработанной тренировкой) может служить так называемая дыхательная синергия. Она состоит в следующем. У спокойно стоящего человека при вдохе и выдохе происходит заметное смещение частей тела. Однако эти смещения никак не отражаются на положении центра тяжести тела в целом. Причина этого состоит в том, что при вдохе одновременно с отклонением туловища назад происходит отклонение таза вперед (при выдохе - картина обратная). Таким образом, смещения различных частей тела при дыхании не независимы, а согласованы между собой так, что они компенсируют друг друга (рис. 4). При некоторых мозговых заболеваниях эта синергия разрушается, и тогда центр тяжести стоящего человека колеблется в соответствии с ритмом дыхания.
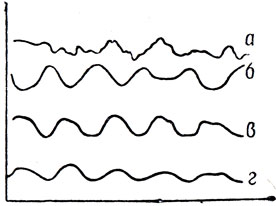
Рис. 4 Дыхательная синергия:
а - колебания центра тяжести стоящего человека; б - колебания туловищного угла;
в - колебания в тазобедренном суставе; г - ритмика дыхания
Мы уже упоминали, что одни синергии - врожденные, а другие возникают в результате обучения. Можно сказать, что обучение человека тем или иным движениям, например ходьбе на лыжах, плаванию и т. п. и состоит, собственно в отработке у него соответствующих синергий. Беспомощные движения человека, впервые попавшего в воду или только что ставшего на лыжи, - это неумение справиться в непривычных условиях с тем множеством степеней свободы, которое наше тело имеет.
При сложных движениях происходит последовательное чередование различных синергий. Таким образом, синергии - это те «готовые детали», из которых мы строим все наши движения.
Группировка параметров системы, имеющей много степеней свободы, в «блоки» и связанное с этим существенное уменьшение числа независимых параметров является, по-видимому, одним из общих и эффективных методов управления такими системами. А то обстоятельство, что эта группировка меняется в зависимости от выполняемой двигательной задачи, делает очень богатым и разнообразным запас тех действий, которые мы способны выполнять.
Многоуровневая организация системы управления
Итак, один из эффективных способов управления многопараметрическими системами состоит в том, чтобы группировать эти параметры в крупные блоки и управлять целыми такими блоками. Другой общий принцип управления такими сложными системами - распределение задачи между несколькими уровнями. Это означает следующее. Будем для определенности снова говорить о построении движений. Для того чтобы мы выполнили некоторое движение, скажем, взяли со стола чашку, нужна согласованная работа многих мышц, каждая из которых, в свою очередь, состоит из большого количества отдельных волокон - «двигательных единиц», управляемых соответствующими мотонейронами. Ясно, что, выполняя такое движение, мы вовсе не обдумываем работу каждой отдельной мышцы и тем более не управляем сознательно каждой двигательной единицей. Высший отдел нервной системы (большие полушария головного мозга) ставит лишь общую задачу - переместить чашку рукой из одного заданного положения в другое. Однако оно не контролирует действия отдельных двигательных единиц, подобно тому как командующий армией, ставя перед своими войсками некую общую задачу, не предписывает каждому солдату, что именно он должен делать в каждый момент сражения.
Детализация построения того или иного движения происходит на уровнях более низких, чем кора больших полушарий, в частности в различных отделах спинного мозга. Более того, в некоторых случаях (например, когда мы отдергиваем руку, случайно коснувшись горячего предмета) вся команда исходит от этих нижележащих уровней: мы еще, как говорится, «не успеем подумать», а рука уже отдернута.
Такое многоуровневое построение управления гораздо экономичнее, чем жесткое централизованное, при котором какой- то центральный орган точно предписывает действия каждой из составляющих систему частей. Действительно, в последнем случае сам управляющий орган оказался бы настолько сложным, что едва ли смог бы функционировать. Попробуйте-ка представить себе штаб армии, который разрабатывает в деталях поведение каждого солдата во время боя! Впрочем, еще труднее было бы представить себе живой организм, в котором все процессы, вплоть до внутриклеточных, определялись единым центром.
Принцип наименьшего взаимодействия. Локальное управление сложными системами
Для таких сложных биологических систем, как, например, целый организм, характерна структура, допускающая выделение в них отдельных, относительно независимых подсистем. Для каждой такой подсистемы совокупность всех остальных подсистем образует своего рода «внешнюю среду», в которой эта подсистема существует. Функционирование такой составной системы может быть организовано по «централизованному» принципу - каждой подсистеме предписывается определенное поведение. Мы уже говорили о неэффективности такого управления в сложных системах. Более соответствует реальному положению дел другая схема, которую можно назвать схемой локального управления. Это означает, что для подсистем, о которых идет речь, «сверху» устанавливаются лишь некоторые общие «правила взаимодействия», а каждая подсистема функционирует так, чтобы ее взаимодействие с остальными подсистемами (и с внешней средой) было в некотором смысле оптимальным.
Эти идеи были развиты несколько лет тому назад в работах И. М. Гельфанда и М. Л. Цетлина, которые выдвинули так называемый «принцип наименьшего взаимодействия», аналогичный известным в механике вариационным принципам. Согласно этому принципу каждая подсистема в живом организме функционирует так, чтобы ее взаимодействие со всей системой и с окружающей средой было возможно меньшим. В такого рода понятиях можно описать ряд физиологических явлений, например, таких, как синхронизация работы нервных или двигательных элементов и т. п. Вместе с тем следует подчеркнуть, что пока еще все соображения, связанные с принципом наименьшего взаимодействия, носят весьма неопределенный, предварительный характер, поскольку для живых систем мы, как правило, не можем точно указать, как это взаимодействие можно выразить математически.
Проиллюстрируем понятие локального управления на примере одной задачи, взятой, правда, не из биологии, а из техники. Представим себе, что у нас имеется n пар радиостанций и внутри каждой пары происходит передача и прием, а станции, относящиеся к разным ларам, друг с другом не связываются. Если эти пары радиостанций не очень удалены друг от друга, то они создают друг для друга помехи, затрудняющие, в той или иной степени, связь. Качество радиосвязи для каждой пары можно охарактеризовать отношением мощности сигнала к мощности шума. Если какая-то пара считает качество связи недостаточно хорошим, то она может увеличить мощность передачи. Однако это усилит помехи, создаваемые данной радиостанцией для других; они, в свою очередь, увеличат мощность передачи, а тем самым увеличат и помехи для той станции, о которой идет речь. Таким образом, эта станция может в результате увеличения мощности передачи не улучшить, а ухудшить свое положение. Можно, конечно, попытаться еще более увеличить мощность, но то же самое могут сделать другие станции. В системе возникнет лавинный режим нарастания мощностей, напоминающий некую веселую компанию, в которой каждый старается перекричать всех остальных, но все голоса тонут в общем шуме.
Возвращаясь к нашим радиостанциям, поставим следующий вопрос: какие же разумные способы регулирования мощностей, выводящие всю систему в целом на некоторый целесообразный устойчивый режим, можно предложить? Подчеркнем еще раз, что регулировка должна быть локальной, т. е. каждой станции известны лишь собственная мощность и собственное отношение сигнал/шум, а центра, в котором собирались бы все сведения и вырабатывались рекомендации для всей системы, не существует. Мы не будем здесь заниматься этой проблемой подробно, но укажем, что рассматриваемая задача допускает точное математическое решение. В принципе оно может быть основано на том, что на каждой станции оператор, произведя некоторое изменение мощности, должен нотой в течение определенного времени наблюдать, как это изменение отразилось на качестве его связи. Возникающие здесь вопросы и трудности довольно типичны для общей проблемы локального регулирования сложных систем.
Таковы некоторые общие принципы, с которыми мы сталкиваемся, рассматривая проблему эффективного управления сложными многопараметрическими системами.
С благодарностью к источнику: Библиотека по математике. Математика в биологии
The post Некоторые общие принципы управления большими системами first appeared on Математику в помощь.
]]>The post «Космическая музыка»: от Платона до Кеплера first appeared on Математику в помощь.
]]>Современник, даже когда его влечет старина, склонен считать своих предков людьми простодушными и недалекими. Он замечает в них прежде всего то, чего им не хватало с современной точки зрения, и обычно не замечает того, чего ему самому не хватает по сравнению с ними.
М. Алпатов
В наш бурный век космической тематикой вряд ли кого удивишь, тем более читателей, родившихся во время полетов человека в космос. "Космическая музыка" - это нечто вибрирующее, электронное из фильмов о летающих тарелках и инопланетянах - тоже стала привычной. Но вот то, что задолго до нашей эры, во времена, когда человечество "летало" только на восковых крыльях в мифах о Дедале и Икаре, была своя "космическая музыка", многим, возможно, покажется удивительным.
По преданию, слово "космос", первоначально означавшее "прекрасно устроенный", ввел в обиход Пифагор. "Скажи мне, ...разве есть что-либо стройное и прекрасное, что не было бы подражанием миру. Отсюда имя "Космос", которое греки дали ему, - вторил Пифагору через полтысячелетия Апулей. Из античности термин "космос" перешел в современную науку как синоним слова "вселенная".
Итак, космос для пифагорейцев - это гармоничное, пропорциональное строение мира. Сами же пропорции, как мы уже видели, мыслились греками музыкально поэтому и весь космос оказывался гармонично устроенным и музыкально звучащим телом. Согласно пифагорейским представлениям, планеты располагались на небесных сферах и совершали вместе с ними круговое вращение. Тогда, как и все движущиеся тела, вследствие трения об эфир они издавали звуки, которые соединялись в музыкальные созвучия. Так Рождалась чудесная музыка - "мировая Музыка", или "гармония сфер", без которой мир бы распался. Сама же музыка - это первое из искусств, доставляющих людям радость,- являлась, по их мнению, отражением гармонии, царящей среди небесных сфер.
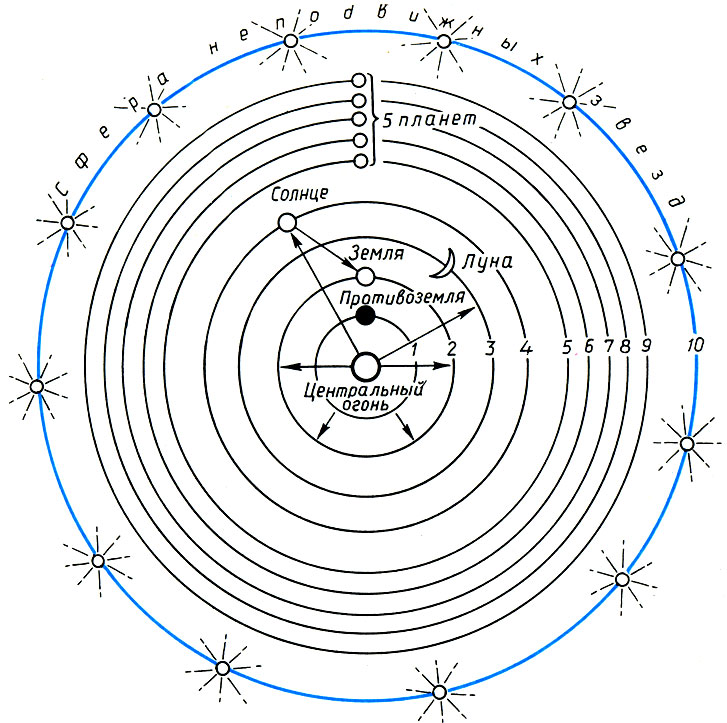
Система мира по Филолаю
Учение о музыке сфер - самый туманный и вместе с тем поэтичный мотив пифагорейской эстетики. Он имел тысячи вариантов, оттенков и тысячелетнюю традицию, начиная от Пифагора и Платона до "Гармонии мира" Иоганна Кеплера, написанной уже в XVII веке. Разумеется, учение о "космической музыке" для нас, современников космических полетов, не более как красивая сказка, и расскажем мы эту сказку, чтобы показать, насколько сильным было музыкальное начало во всем античном мировоззрении. Кроме того, как и во всякой сказке, в этом учении рассыпаны зерна истины, позволяющие увидеть глубокие параллели в развитии человеческой мысли.
Первое письменное изложение пифагорейских идей появилось около 420 г. до н. э. в сочинении "О природе". "Природа, сущая в космосе, гармонично слажена из беспредельного и определяющих начал. Так устроен весь космос и все, что в нем" - так начинается эта книга, приписываемая Филолаю, ученику непосредственного ученика Пифагора - Гиппаса. Здесь же мы находим и первое письменное свидетельство о музыкально-числовом строении космоса.
По Филолаю, центром мироздания является некий Центральный Огонь, вокруг которого на десяти концентрических сферах в порядке удаления от него вращаются так называемая Противоземля, затем Земля, Луна, Солнце, пять планет (Меркурий, Венера, Марс, Юпитер, Сатурн - их последовательность Филолаем не указана)* и, наконец, Сфера неподвижных звезд. Центральный Огонь и Противоземля невидимы, ибо заслонены поверхностью Земли. Солнце, по Филолаю, только отражает свет и тепло Центрального Огня. Противоземля же введена им отчасти для объяснения солнечных затмений, отчасти для достижения требуемой числовой мистикой "священной десятки" - вместе с Противоземлей сфер получается десять. В пифагорейской системе Земля не является центром мироздания, а вместе с другими планетами движется вокруг Центрального Огня - прообраза Солнца. Вот почему, когда в XVI веке церковь развернула борьбу с гелиоцентрическим учением Коперника, это учение именовалось пифагорейским.
* (Напомним, что остальные три планеты Солнечной системы - Уран, Нептун и Плутон - были открыты лишь в XVIII, XIX и XX веках соответственно. )
Внутреннее устройство пифагорейского космоса напоминало своеобразную музыкальную шкатулку: каждая из десяти движущихся сфер издавала некоторый звук. "Когда несутся Солнце, Луна и еще столь великое множество таких огромных светил со столь великой быстротою, невозможно, чтобы не возникал некоторый необыкновенный по силе звук", - утверждает неизвестный пифагорейский автор, возможно Филолай. Высота звука определялась скоростью движения сферы, зависящей от расстояний между сферами, а последние находились в той же пропорции, что и интервалы музыкальной гаммы. Таким образом, колеблемый движением сфер эфир издает чудесную мировую музыку. Однако человеческое ухо не слышит этой ни с чем не сравнимой музыки. Как рожденный на берегу моря человек перестает в конце концов различать беспрестанный рокот волн, так и слух человека привык и не замечает гармонического звучания небесных сфер.
Итак, согласно пифагорейцам, небесная музыка изначально незримо живет в человеке. Вот почему человеческая душа охотно откликается на обычную земную музыку, которая является лишь подражанием небесной; вот почему из всех искусств музыке в античности отводилась исключительная роль.
Дальнейшее развитие пифагорейское учение о гармонии сфер получило в трудах Платона. Платоновский диалог "Тимей", эта квинтэссенция древнего пифагорейства, является лучшим образцом античной космологии. Однако многое в "Тимее" изложено туманными и заумными намеками. Уже в древности эти места вызывали бесконечные споры, разночтения и комментарии, которые длятся и до сего времени.
Платон исходит из геоцентрической системы космоса: центром мироздания для него является неподвижная Земля, вокруг которой на семи сферах* вращаются Луна, Солнце, Венера, Меркурий, Марс, Юпитер, Сатурн. Далее следует сфера неподвижных звезд. Как видим, несостоятельность Центрального Огня и Противоземли ко времени Платона была уже осознана.
*(Отсюда пошло выражение "Быть на седьмом небе", обозначающее высшую степень блаженства.)
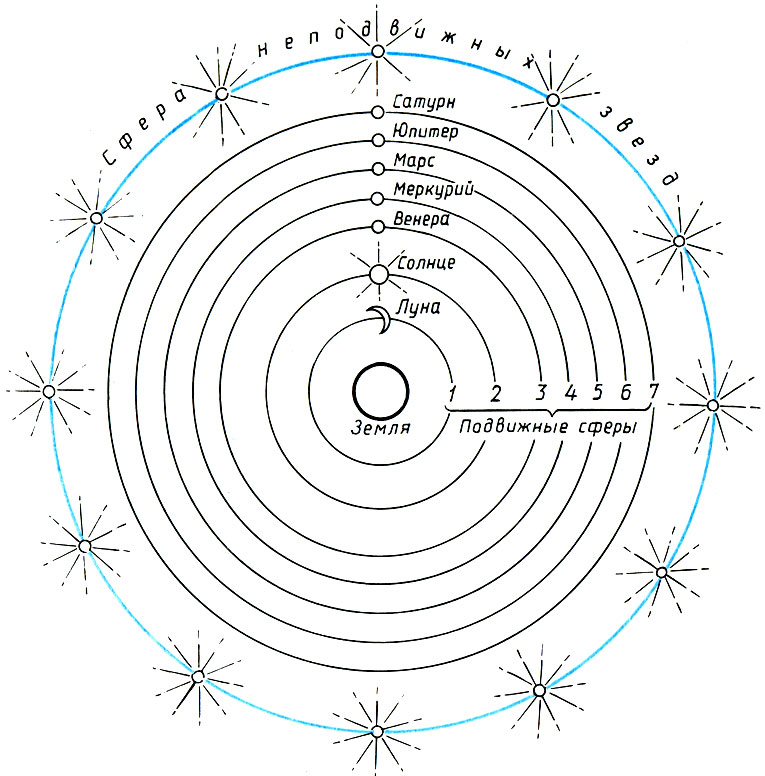
Система мира по Платону
На базе этой системы мироздания Платон развивает теорию небесного гептахорда - семиструнника, т. е. теорию семи подвижных сфер, настроенных в музыкальных отношениях. Согласно Платону, творец Вселенной - Демиург, создав вещество Вселенной, разделил его на две части: одна часть пошла на построение сферы неподвижных звезд, а вторая была математически строго разделена на семь частей для образования сфер Луны, Солнца и пяти планет. По этому поводу в "Тимее" Платона мы читаем: "Делить же он начал следующим образом: прежде всего отнял от целого одну долю, затем вторую - вдвое большую, третью - в полтора раза больше второй и в три раза больше первой, четвертую - вдвое больше второй, пятую - втрое больше третьей, шестую - в восемь раз больше первой, а седьмую - больше первой в двадцать семь раз". В результате получился ряд чисел
описывающий гармонию небесных сфер, или небесный гептахорд. Однако ни порядок расположения сфер, несущих светила, ни порядок отсчета чисел в ряде (7.1) Платоном указан не был. Поэтому на протяжении последующих двух тысячелетий члены платонова гептахорда имели самую разнообразную физическую интерпретацию.
Самым простым и соблазнительным было трактовать числа (7.1) как относительные расстояния от Земли до Луны, Солнца, Венеры, Меркурия, Марса, Юпитера и Сатурна соответственно. Тогда эти числа представляли и относительные высоты тонов, так как высота тона, издаваемого сферой, мыслилась пропорциональной скорости вращения сферы, а скорость вращения - пропорциональной расстоянию до неподвижной Земли. Таким образом, чем дальше находилась планета от Земли, тем больше была ее скорость и тем выше издаваемый ею тон. Скорее всего, эти рассуждения были навеяны простым опытом: камень, раскручиваемый на веревке, со свистом разрезает воздух и прекрасно демонстрирует все описанные закономерности. Правда, при такой трактовке относительное расстояние до Марса (9) получалось больше, чем до Юпитера (8), и, чтобы "исправить" эту ошибку, числа 9 и 8 в (7.1) просто переставили. Вот почему во многих текстах платонов гептахорд фигурирует в искаженном виде: 1, 2, 3, 4, 8, 9, 27.
И все-таки оставалось непонятным: откуда вообще взялся этот странный ряд чисел? Это загадка, которую исследователи, начиная с Аристотеля, чаще всего трактовали как некий курьез, если не просто глупость, не требующую даже разъяснений. "Однако,- как справедливо замечал А. Ф. Лосев,- такой антиисторический подход не может быть у современного исследователя, который, конечно, настолько далек от древнего пифагорейства, что даже не испытывает потребности его критиковать, а должен рассмотреть его со всеми объективно-историческими причинами, делающими его существование понятным".
Ключ к Платонову гептахорду, по-видимому, спрятан в самом пифагорейском понимании числа, а именно: единицы - как символа неделимого начала, двойки - как символа неопределенной бесконечности и тройки - как символа определенности. Но для Платона это слишком просто, и в качестве символа беспредельности он берет куб со стороной 2. Тогда его геометрические параметры (длина, площадь грани и объем) дают числа 2, 4, 8. А в качестве символа определенности Платон берет куб со стороной 3 и параметрами 3, 9, 27. Тогда взаимное переплетение этих двух троек чисел плюс начало всего - единица - и дают то единство "беспредельного и определяющих начал", о которых говорил Филолай.
Интересную реконструкцию платонова космоса в 1985 г., предложил инженер С.В. Житомирский. Учитывая, что небесные сферы мыслились Платоном материально, т.е. обладали некоторой толщиной (такое представление сохранилось вплоть до Кеплера), Житомирский трактует числа (7.1) как толщины соответствующих сфер, причем отсчет начинает не от Земли, как это всегда было принято, а, наоборот, от сферы неподвижных звезд. Далее, вспоминая, что на изготовление последней сферы пошло столько же материала, сколько и на все остальные, он полагает толщину сферы неподвижных звезд равной толщинам всех остальных сфер, т.е. 54 = 1 + 2 + 3 + 4 + 9 + 8 + 27. Таким образом получается реконструкция картины платонова космоса, которая согласуется с другими космологическими текстами Платона, а числа гептахорда (7.1) наполняются конкретным геометрическим содержанием:

Земля - Луна - Солнце - Венера - Меркурий - Марс - Юпитер - Сатурн - Небо звезд
Заметим, что и реконструкция Житомирского также страдает изъяном, так как Земля теперь растворилась в сфере Луны. Не будем более погружаться в бездну вопросов Платонова космоса, из которых уже два с половиной тысячелетия ищут выхода, и перейдем к музыкальной стороне учения Платона. Легко видеть, что платонов гептахорд содержит в себе все основные музыкальные интервалы: октаву (2/1), квинту (3/2), кварту (4/3), тон (9/8) и полутон 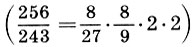 . Объясняется это просто, ибо, как мы увидим в следующей главе, все тона пифагоровой гаммы получаются ходами вверх или вниз по квинтам (3/2), а квинта составлена из отношения тройки и двойки, т. е. из тех чисел, что и платонов гептахорд. С помощью полученных интервалов можно рассчитать строй любого лада. Неудивительно, что Платон утверждает, будто космос настроен в дорийском ладу, этом истинно национальном ладу древних греков, хотя остается непонятным, как получить строй дорийского лада из Платонова гептахорда. Не очень ясно также и то, что на самом деле представляет собой звучание Платонова гептахорда: гармонию или дисгармонию или даже какофонию сфер. Попробуйте решить для себя этот вопрос сами, сыграв гептахорд (7.1), скажем, от ноты До большой октавы: До-до-соль-до1-ре2-до2-ля3.
. Объясняется это просто, ибо, как мы увидим в следующей главе, все тона пифагоровой гаммы получаются ходами вверх или вниз по квинтам (3/2), а квинта составлена из отношения тройки и двойки, т. е. из тех чисел, что и платонов гептахорд. С помощью полученных интервалов можно рассчитать строй любого лада. Неудивительно, что Платон утверждает, будто космос настроен в дорийском ладу, этом истинно национальном ладу древних греков, хотя остается непонятным, как получить строй дорийского лада из Платонова гептахорда. Не очень ясно также и то, что на самом деле представляет собой звучание Платонова гептахорда: гармонию или дисгармонию или даже какофонию сфер. Попробуйте решить для себя этот вопрос сами, сыграв гептахорд (7.1), скажем, от ноты До большой октавы: До-до-соль-до1-ре2-до2-ля3.
Впрочем, все это сегодня уже неважно. Для нас, людей XX века, важно другое: Платон мыслит мировое пространство неоднородным, как неодинаково натянуты струны единого музыкального инструмента. Но ведь эта мысль о неоднородности мирового пространства созвучна выводам из общей теории относительности Альберта Эйнштейна об искривленности пространства - времени и его неоднородности! Более двух тысячелетий, от Платона до Эйнштейна, мировое пространство мыслилось абсолютным и однородным! И вот за этот огромный промежуток времени, практически равный всей истории европейской цивилизации, наука, как и определено законами диалектики, совершает огромный виток по спирали и прежний вывод делается на базе самых современных научных знаний, а старая научная платформа кажется наивной и смешной! Сколько еще таких витков предстоит сделать науке?!
От внешнего строения космоса Платон в "Тимее" переходит к внутреннему его строению, т. е. строению материи. Это знаменитое учение Платона о четырех стихиях - основных компонентах мира и их атомах - Платоновых телах. Менее известно, что это учение также "музыкально", но, прежде чем остановиться на нем, следует сказать несколько слов о самом Платоне и его научных взглядах, что, видимо, поможет понять истоки этого экзотического учения.

Платон (427-347). Римская мраморная копия с греческого оригинала. Ок. 370 до н. э
Платон (427-347 гг. до н. э.) - величайший философ античности, оказавший огромное влияние на развитие всей мировой культуры. Однако Платон был не только философом, создателем первой в истории человечества системы объективного идеализма, "линии Платона", но также и блестящим художником слова, организатором и теоретиком науки, ученым и гражданином города-государства Афины. После казни своего любимого учителя Сократа, болезненно переживая кризис афинской демократии, Платон покинул Афины и около двенадцати лет провел в путешествиях. Вернувшись на родину, Платон основал научную школу - Академию, которая разместилась на купленном для этой цели Платоном участке в роще близ Афин. Роща носила имя древнеаттического героя Академа, откуда и пошло название первой в истории человечества научной школы - Академии.
Платон и его ученики, платоники, были самой влиятельной после пифагорейцев группой мыслителей, а Платонова Академия в течение девяти столетий оставалась центром, влекущим к себе лучшие умы античности. Платон направлял и воодушевлял научную работу. Великие математики Теэтет и Евдокс были друзьями Платона, его учителями в математике и учениками в философии. Великий ученик Платона - Аристотель, будущий учитель и воспитатель Александра Македонского, двадцать лет жизни провел в благотворной атмосфере Академии. Хотя сам Платон и не был математиком, он придавал огромное значение изучению математики, живо интересовался ею и требовал от своих учеников основательных знаний математики, прежде чем посвятить их в свою философию. По преданию, на вратах Академии Платона было начертано: "Негеометр да не войдет!", а одному из начинающих философов, не знавшему математики, Платон сказал: "Уйди прочь! У тебя нет орудия для изучения философии..."
Не останавливаясь на философской системе Платона, отметим только, что, согласно Платону, существуют два мира: материальный несовершенный мир вещей и совершенный мир идей. Законы мира вещей несовершенны и преходящи, тогда как в мире идей господствуют абсолютные и неизменные истины, которые и надлежит изучать философу. Материальный мир есть не более как одна из несовершенных реализаций мира идей, и постигнуть реальный мир можно только с помощью математики идеального мира. То, что идеальный мир основан на математике, сомнений не вызывало. "Знание, к которому стремятся геометры, есть знание вечного, а не того, что тленно и преходяще", - утверждал Платон.
Таким образом, Платон ясно осознавал значение математизации науки, и это именно тот путь, по которому пошло развитие науки в античности и по которому оно продолжает идти сегодня. Однако следует четко различать: то, что Платон видел в математике инструмент познания законов природы, безусловно, верно, но что он считал истинным только мир идей, ложно. Это заблуждение Платона было вызвано тем очевидным фактом, что законы мира вещей открывались лишь путем абстрагирования и идеализации, путем "стирания случайных черт". Потому идеальный мир идей и казался Плауну истинным и непреходящим. Таким образом, идеализм Платона был связан с преувеличением роли разума и недооценки значения опыта.
Показательно, что в наше время стремительной математизации и широчайшего применения ЭВМ, время, когда стало возможным физический эксперимент заменить экспериментом вычислительным и буквально "увидеть" на экране дисплея ЭВМ то или иное физическое явление, некоторые философы-идеалисты пытаются поднять на щит учение Платона. Ответ им сформулирован в статье Ю.А. Жданова "Философские проблемы современного естествознания": "В законах математики отражаются не свойства ума, а свойства всей материи, в том числе и ума. Вот почему эти законы имеют объективное содержание, вот почему они обладают эвристическим характером, вот почему на их основе можно строить научный прогноз и предсказание, проверяя их в последующем практикой". Напомним, что и в начале нашего столетия - времени рождения теории Эйнштейна и бурных потрясений в физике - Философы-идеалисты восклицали: "Материя исчезла, остались одни уравнения!"
Но вернемся в Древнюю Грецию. Теперь нам будет понятно, откуда Платону пришла мысль отождествлять физические элементы (атомы четырех стихий) с геометрическими телами - правильными многогранниками: в геометрии Платон видел ключ к познанию природы. Впрочем, по порядку...
Многогранник называется правильным, если он лежит по одну сторону от плоскости любой его грани, т. е. является выпуклым, и все его грани есть равные правильные многоугольники. Простой подсчет суммы углов при вершине правильного многогранника показывает, что существует только пять правильных многогранников*. Доказательство этого факта имеется в XIII книге "Начал" Евклида, но сам факт был, безусловно, известен Платону, а правильные многогранники знали пифагорейцы задолго до Платона. Форму правильных тел, по-видимому, подсказала древним грекам сама природа: кристаллы поваренной соли имеют форму куба, кристаллы квасцов - октаэдра, а кристаллы пирита - додекаэдра. Последний, как показали раскопки в итальянских Альпах, был любимой игрушкой этрусских детей задолго до нашей эры.
* ( В самом деле, сумма плоских углов s при вершине выпуклого многогранника должна быть строго меньше 360°, а число граней при вершине m≥3. Тогда гранями правильного многогранника могут быть только три плоские фигуры: правильные треугольник, четырехугольник (квадрат) и пятиугольник, ибо уже для шестиугольников s = 120°*3 = 360°. Название правильному многограннику дается по общему числу граней М. Таким образом, из равносторонних треугольников можно составить три правильных многогранника при m = 3, 4, 5 (при m = 6 s = 60°*6 = 360°):
1. Тетраэдр (четырехгранник): m = 3, М = 4.
2. Октаэдр (восьмигранник): m = 4, М = 8.
3. Икосаэдр (двадцатигранник): m = 5, М = 20, а из квадратов и правильных пятиугольников - только по одному при m = 3 (при m = 4 s = 90°*4 = 360° - для квадратов и s = 108°*4 = 432° - для пятиугольников).
4. Гексаэдр (шестигранник), или куб: m = 3, М = 6.
5. Додекаэдр (двенадцатигранник): m = 3, М = 12.
В любом выпуклом многограннике числа вершин L, граней М и ребер N связаны формулой Эйлера L + M - N = 2.)
Правильные многогранники всегда восхищали пытливые умы симметрией, простотой и мудростью своих форм. Леонардо да Винчи любил изготовлять из дерева каркасы правильных тел и преподносить их в виде подарка различным знаменитостям. К сожалению, мы не можем подробнее остановиться на массе любопытных геометрических свойств и физических приложений правильных тел. это выходит за рамки нашего разговор* а тем, кто заинтересуется ими, мы рекомендуем прочитать книгу К. Левитил "Геометрическая рапсодия".
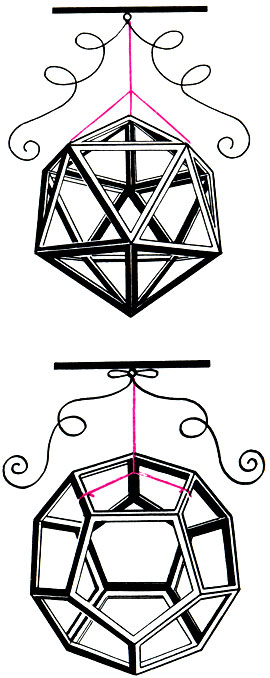
Рисунки тел Платона, выполненные Леонардо да Винчи к книге Луки Пачоли 'О божественной пропорции'. Венеция. 1509
Ко времени Платона в античной философии уже созрела концепция четырех элементов (стихий) - первооснов материального мира: огня, воздуха, воды ц земли. Огонь и землю Платон считает основными компонентами для образования космоса: "...всему, что имело произойти, надлежало, конечно, быть телесным, видимым и осязаемым. Но быть видимым ничто не может без посредства огня, точно так же и осязаемым ничто не может быть без чего-нибудь твердого, твердым же ничто не может быть без земли (Тимей)". Между основными стихиями помещаются две средние - вода и воздух, и все они связываются музыкальными отношениями. Атомам земли Платон придает форму куба, так как и земля, и куб отличаются неподвижностью и устойчивостью. Атомам воды - форму икосаэдра, так как вода отличается текучестью, а из всех правильных тел икосаэдр - наиболее "катящийся". Атомам воздуха - форму октаэдра, ибо воздух движется взад и вперед и октаэдр как бы направлен одновременно в разные стороны. Атомам огня - форму тетраэдра как наиболее острого, мечущегося в разные стороны. Не у дел остался пятый правильный многогранник - додекаэдр. Для него Платон вводит пятый элемент - "пятую сущность"* - мировой эфир, атомам которого придается форма додекаэдра как наиболее близкого к шару - самому совершенному по форме телу. С тех пор правильные многогранники называются также платоновыми телами.
* (Пятая сущность - по-латыни квинтэсенция - у средневековых алхимиков стала означать тончайший элемент, составляющий якобы сущность вещей. В настоящее время квинтэссенция - синоним самого главного, и наиболее существенного.)
Далее, поскольку в музыкальных отношениях греки видели основу "всеобщей гармонии", Платон устанавливает эти отношения не только для космических тел (гармония сфер), но и для самих элементов, из которых состоит космос. По Платону, отношение основных элементов - атомов земли к атомам огня - равно октаве (2/1), отношение атомов земли и воды, а также воздуха и огня равно кварте (4/3) и т. д. Несмотря на любовь Платона к геометрии, эти отношения не имеют никакой математической базы. Ими не связаны ни число вершин Платоновых тел, ни объемы этих тел, вписанных одно в другое, ни число ребер или граней.
Заметим, что поиск музыкальных отношений в геометрических образах сильно увлекал античных исследователей. Не случайно из множества первоклассных открытий Архимед больше всего ценил открытие отношения объемов и площадей поверхностей цилиндра и вписанного в него шара, равного 3/2, т. е. квинте.
Но и в отжившем учении Платона об атомах четырех стихий есть своя внутренняя мудрость. Стремление свести сложные природные явления к простым неразложимым компонентам остается содержанием и современного естествознания. Сейчас известно чуть более ста атомов элементов, из которых состоят все встречающиеся в природе вещества. Сверхзадачей современной физики является выявление "кирпичиков мироздания" - элементарных частиц - первичных, неразложимых далее частиц, из которых состоит вся материя. Еще в начале XX века считалось, что таких частиц три: электрон, протон и нейтрон. Однако катастрофический рост числа открываемых элементарных частиц привел во второй половине XX века к пересмотру воззрений об их элементарности. Сегодня есть основания считать, что такие "экс-элементарные" частицы, как протоны, нейтроны, мезоны, гипероны и др., состоят из различных комбинаций трех типов кварков* (либо пар кварк - антикварк) - новых "кирпичиков мироздания".
* (Любопытна история возникновения термина. Это название заимствовано американским физиком М. Гелл-Маном, высказавшим в 1964 г. гипотезу о существовании трех неизвестных частиц, из романа современного английского писателя Дж. Джойса "Поминки по Финегану". Хотя по-немецки "кварк" - это "творог", в романе слово означает нечто таинственное и непонятное. Герою романа снится сон, где чайки кричат: "Три кварка для мастера Марка". Так слово, изобретенное писателем Джойсом, стало едва ли не важнейшим термином современной ядерной физики. Вот они, узы науки и искусства!)

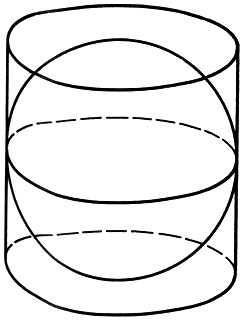
Теорему об отношении объемов и площадей поверхности цилиндра и вписанного в него шара Архимид считал своим высшим достижением.
По завещанию Архимеда чертеж этих фигур был выполнен на его могильном камне
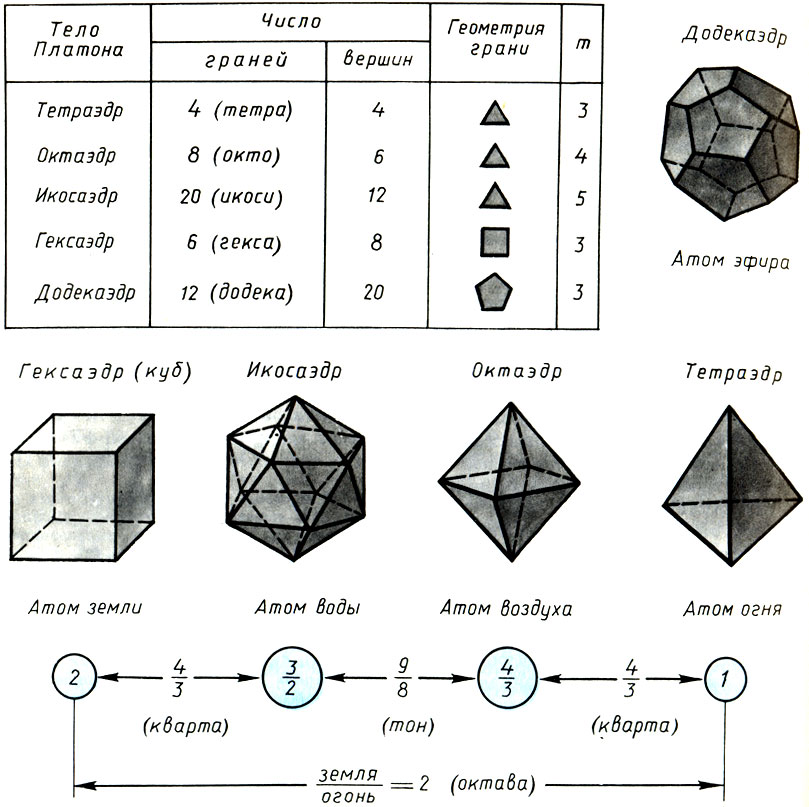
Непреходящие математические свойства правильных многогранников (таблица) и их наивная физическая интерпретация по Платону
Еще более современным выглядит стремление Платона видеть элементы материи в виде правильных симметричных тел. Современная наука все глубже проникает в тайну того, что внешние проявления симметрии - от симметрии кристаллов и снежинок до симметрии молекул ДНК - есть следствие симметрии тех фундаментальных законов, которые управляют всеми процессами физического мира. Таким образом, то, что на заре цивилизации античные философы видели атомы в виде симметричных геометрических тел должно вызывать не саркастическую усмешку, а, скорее, удивление.
Учения о четырех стихиях и гармонии сфер из античности перешли в средневековье. Народное творчество, фантазия средневековых алхимиков и воображение поэтов населили четыре Платоновы стихии мифическими существами - духами. Так появились подземные человечки - гномы или кобольды - духи земли; златокудрые русалки - ундины - с рыбьим хвостом вместо ног - духи воды; прекрасные существа, населяющие атмосферу, ростом не более дюйма с шапочкой из цветка на голове - сильфы или эльфы - духи воздуха; наконец, духи огня - саламандры, пляшущие в огне в виде ящериц. Страшные карлики-гномы охраняют подземные богатства, они сказочно богаты, любят дразнить людей, но чаще помогают им. Красавицы-ундины вечерами расчесывают на берегу свои пышные волосы. Однако они опасны, так как могут очаровать своей красотой и пением пылкого юношу и увлечь его в подводное царство. Танцы и музыка - любимое занятие эльфов, а если музыкант начнет играть мелодию эльфов, то он не сможет остановиться, пока не доиграет ее до конца. Знакомые с детства сказки Андерсена "Дюймовочка" и "Русалочка", сказка братьев Гримм "Белоснежка и семь гномов", комедия Шекспира "Сон в летнюю ночь", баллада Гёте "Лесной царь", поэма Жуковского "Ундина" и многие стихотворения многих авторов навеяны этими легендами. Так отжившая научная теория превращалась в красивую сказку.
Саламандра, жгись,
Ундина, вейся,
Сильф, рассейся,
Кобольд, трудись!
Кто слышит впервые
Про эти стихии,
Их свойства и строй,
Какой заклинатель?
Кропатель пустой!
(Гёте. "Фауст")
Не менее популярным оставалось в средние века и учение о гармонии сфер. Вообще, считалось, что законы мироздания в основе своей являются музыкальными законами. Мысль эта прочно вошла в сознание не только средневековых ученых-схоластов, но и поэтов. Гармония сфер звучит в "Божественной комедии" великого Данте, написанной в начале XIV века:
Когда круги, которых вечный ход
Стремишь, желанный, ты, мой дух
призвали Гармонией, чей строй тобой живет,
Я видел - солнцем озарились дали
Так мощно, что ни ливень, ни поток
Таких озер вовек не расстилали.
("Рай", песнь I)
Несмотря на увлечение Данте числовой мистикой, архитектура его бессмертной поэмы является непревзойденным образцом математической строгости. Поэма делится на три части: "Ад", "Чистилище" и "Рай". В каждой части - 33 песни, что вместе со вступительной песнью дает 100 песен - квадрат "священного" числа 10. В каждой части и каждой песне практически одинаковое число стихов (строк), а каждая часть заканчивается одним и тем же словом - stella (звезда, светило). Описываемое Данте мироздание построено на числе 9 - квадрате символа определенности числа 3: в Аду - 9 кругов, в Раю - 9 небес, семь кругов Чистилища и два уступа предчистилища также дают число девять и т. д.
Боттичелли. Иллюстрация к 'Божественной комедии' Данте. 1492-1497. Данте, влекомый Беатриче, взирает на геоцентрическую систему мироздания
Заключительные аккорды "космической музыки" прозвучали в работах Иоганна Кеплера (1571 -1630) - выдающегося немецкого математика, физика, астронома. Следуя пифагорейско-платоновской традиции, Кеплер верил, что в основе мироздания лежат простые числовые соотношения и совершенные геометрические формы. Но Кеплер поставил и вопросы, достойные отца современного естествознания: почему планет (известных в то время) только шесть? Почему их орбиты имеют те, а не иные параметры?
Сначала молодой учитель математики Иоганн Кеплер тщетно ищет между параметрами планетных орбит простые числовые отношения. Но вдруг... Решая с учениками какую-то геометрическую задачу, он начертил на классной доске равносторонний треугольник со вписанной и описанной окружностями.
Внезапно его озарила мысль, что планетные орбиты связаны между собой посредством геометрических фигур. Однако расчеты показали, что плоские геометрические фигуры не удовлетворяли этой идее. Новые разочарования... "И вот я снова устремился вперед. Зачем рассматривать фигуры двух измерений для пригонки орбит в пространстве? Следует рассмотреть формы трех измерений...", - вспоминал впоследствии Кеплер. Новые поиски и новое озарение: существует только шесть планет и, следовательно, пять промежутков между ними. Но и Платоновых тел только пять! Как трудно было допустить, что это простое совпадение!.. "Я еще не имел ясной идеи о порядке, в котором следует расположить правильные тела... День и ночь я проводил за расчетами... Через несколько дней все стало на свои места." Какой накал страстей в этих записях Кеплера!
Вскоре двадцатичетырехлетний учитель издает маленькую книжку с вычурным названием, как требовала мода того времени,- "Предвестник космографических исследований, содержащий тайну мироздания относительно чудесных пропорций между небесными кругами и истинных причин числа и размеров небесных сфер, а также периодических движений, изложенный с помощью пяти правильных тел Иоганном Кеплером из Вюртемберга, математиком достославной провинции Штирии", или "Mysterium Сosniographicum" ("Тайна мироздания"), как любил называть ее сам Кеплер. Книга эта содержала формулу открытия Кеплера: в сферу орбиты Сатурна Кеплер вписывает куб, в куб - сферу Юпитера, в сферу Юпитера - тетраэдр, и так далее последовательно вписываются друг в друга сферы Марса - додекаэдр, сфера Земля - икосаэдр, сфера Венеры - октаэдр и сфера Меркурия. В центре всей системы коперниканец Кеплер помещает Солнце*. Тайна мироздания кажется раскрытой! Вселенная устроена на основе единого геометрического принципа!
* (Для каждого правильного многогранника существует вписанная сфера, касающаяся центров каждой грани, и описанная сфера, проходящая через все вершины, причем центры этих сфер совпадают. Таким образом, все построенные Кеплером сферы имеют общий центр.)
Что же показали математические расчеты? Конечно, совпадение с данными Коперника по радиусам планетных орбит было поразительным, но все-таки не столь точным, как того хотелось бы педантичному Кеплеру**. Особенно много хлопот доставила Кеплеру сфера Меркурия, которую в конце концов пришлось вписать в октаэдр так, чтобы она касалась не граней, а середины ребер последнего. Остальные незначительные расхождения между теорией и опытными данными Кеплер объяснил тем, что реальные планетные сферы имеют некоторую толщину, что и позволило "выбрать" эти расхождения.
** (Заинтересовавшийся читатель может легко воспроизвести эти расчеты. Например, для куба с ребром а имеем R = a√3/2, r = a/2, откуда R/r = √3 1,732. Современные усредненные pадиусы орбит Сатурна и Юпитера соответственно равны Rс = 1,427*109 км и Rю = 0,788*109 км, откуда Rс/Rю= 1,834. По Коgерyику, Rс/Rю= 1,758.)
1,732. Современные усредненные pадиусы орбит Сатурна и Юпитера соответственно равны Rс = 1,427*109 км и Rю = 0,788*109 км, откуда Rс/Rю= 1,834. По Коgерyику, Rс/Rю= 1,758.)
Однако червь сомнения поселился в Душе Кеплера. Можно сказать, что оставшиеся тридцать лет жизни Кеплер посвятил "спасению" своей теории от самого себя. Эта работа привела к открытию истинных астрономических законов - трех знаменитых законов Кеплера, на базе которых Ньютон построил свою теорию тяготения. Сам же Кеплер в полной мере не осознал своих настоящих открытий и до конца жизни более всего любил свою первую работу.
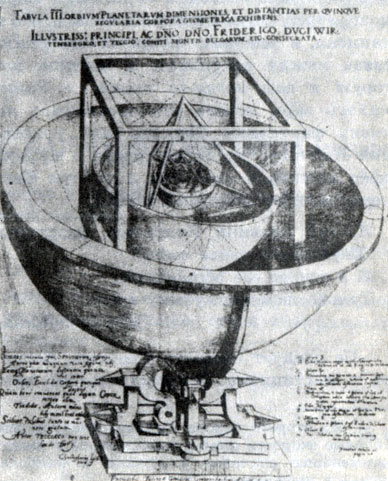
Космический кубок Кеплера, Иллюстрация Иоганна Кеплера из его книги 'Тайна мироздания'. Тюбинген. 1596
Не забыл Кеплер и о самой "музыке" сфер. Поискам гармонических соотношений посвящена одна из глав книги "Гармония мира" (1619), которую он считал своей вершиной: "жребий брошен. Я написал книгу либо для современников, либо для потомков..." Кеплер установил семь основных гармонических интервалов (консонансов): октаву (2/1), большую сексту (5/3), малую сексту (8/5), чистую квинту (3/2), чистую кварту (4/3), большую терцию (5/4) и малую терцию (6/5), из которых он выводит весь звукоряд как мажорного, так и минорного наклонения. После долгих поисков гармонических соотношений "на небе", проделав огромную вычислительную работу, Кеплер наконец установил, что отношения экстремальных (наибольших и наименьших) угловых скоростей* для некоторых планет близки к гармоническим: Марс - 3/2, Юпитер - 6/5, Сатурн - 5/4. "Солнце гармонии засияло во всем блеске... Небесные движения есть не что иное, как ни на миг не прекращающаяся многоголосая музыка". И здесь Кеплера не оставляет буйная фантазия. Небольшие расхождения теории и эксперимента он объясняет тем, что небесный секстет должен звучать одинаково согласованно и в миноре, и в мажоре, а для этого ему необходимо иметь возможность перестраивать свои инструменты. Далее Кеплер утверждает, что Сатурн и Юпитер "поют" басом, Марс - тенором, Земля и Венера - альтом, а Меркурий - дискантом. Никаких математических "доказательств" здесь он не приводит. Да и сам Кеплер устал в поисках всеобщей гармонии: "Мой мозг устает, когда я пытаюсь понять, что я написал, и мне уже трудно восстановить связь между рисунками и текстом, которую я сам когда-то нашел..." Занималась заря нового естествознания: на смену фантазиям Кеплера шли уравнения Ньютона. Красивая сказка о музыке сфер доживала свой век, и работы Кеплера были ее лебединой песней.
Я, как древний Коперник, разрушил
Пифагорово пенье светил
И в основе его обнаружил
Только лепет и музыку крыл.
(Н. Заболоцкий)
* (Из второго закона Кеплера следует, что угловые скорости планет непостоянны и имеют наименьшее значение в афелии и наибольшее - в перигелии.)
Не следует спешить обвинять Кеплера в мистицизме, числовых спекуляциях и увлечении отжившими античными теориями. Правильнее видимо, вспомнить о времени, в которое он жил и творил: XVI век закончился костром на площади Цветов в Риме, где 17 февраля 1600 Г. был сожжен Джордано Бруно. Следует вспомнить трагическую историю матери Кеплера, Катерины Кеплер, которую публично объявил ведьмой и процесс над которой тянулся долгие 6 лет. Обвиняемую заковывали в цепи, ставили перед палачом с орудиями пыток, и только искусные действия ее сына Иоганна, который сам вел защиту, позволили выиграть процесс у церковных мракобесов. "Арестованную, к сожалению, защищает ее сын, господин Иоганн Кеплер, математик",- свидетельствовал судебный писец. Только в родном городе Кеплера Вейле с 1615 по 1629 г. ужасная смерть постигла 38 "колдуний". Вот в какое время рождалось современное естествознание!
"Мы имели дело с человеком тонких чувств, всецело и страстно увлеченным поиском пути к более глубокому проникновению в сущность явлений природы, с человеком, который, несмотря на внутренние и внешние трудности, сумел достичь поставленной перед собой возвышенной цели" - так характеризовал личность Кеплера Альберт Эйнштейн, Кеплер XX века, по справедливому определению физиков наших дней.
Заканчивая наше необычное "музыкальное обозрение", перенесемся в 20-е гг. XX века, когда вновь неожиданно зазвучало "пифагорово пенье светил". Согласно теории Нильса Бора, развитой им в 1913 г., движение электрона вокруг атомного ядра возможно только по избранным "разрешенным" орбитам, двигаясь по которым электрон вопреки законам классической электродинамики не излучает энергии, но может скачком переходить с одной орбиты с энергией Ei на другую "дозволенную" орбиту с энергией Еk, испуская (i>k) или поглощая (i<k) при этом порцию ("квант") электромагнитной энергии с частотой
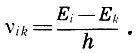 (7.2)
(7.2)
h - постоянная Планка.
В простейшем случае атома водорода, содержащего один электрон, энергия n-го энергетического уровня равна
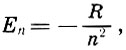 (7.3)
(7.3)
R - постоянная Ридберга.
Здесь n = 1, 2, 3,... называется главным квантовым числом. Тогда совокупность частот, излучаемых атомом водорода при переходе с верхнего энергетического уровня на нижний (i>k), определяет спектр испускания данного атома и каждому такому переходу соответствует своя спектральная линия. Для атома водорода согласно формулам 7.2, 7.3 получаем совокупность спектральных линий с частотами
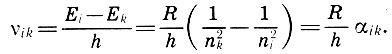
При переходе со второго, третьего и т. д. энергетических уровней ni = 2, 3, 4... на первый nk = 1 получается так называемая "спектральная серия Лаймана", для которой α21=3/4, α31=8/9, α41 = 15/16. Но ведь это кварта (3/4), тон (8/9) и полутон в чистом строе (15/16)! "Таким образом,- писал А. Эйнштейн,- мы открыли некоторое подобие между колебанием струны и атомом, испускающим излучение".
"То, что нам сегодня удается понять на языке спектров,- это истинная музыка атомных сфер, созвучие целочисленных отношений, все возрастающие порядок и гармония при всем их многообразии - так восторженно отзывался о квантовой теории немецкий физик и математик Арнольд Зоммерфельд (1868-1951).- ... Она представляет собой тот полный таинства инструмент, на котором природа исполняет спектральную музыку и ритмом которого она управляет строением атома и атомных ядер".
Итак, обыкновенная музыкальная гамма увлекла нас вслед за Пифагором, Платоном и Кеплером в путешествие по просторам космоса. Мы узнали, что "пифагорово пенье" услышали и физики XX века, но уже не в космосе, а в противоположной стихии - микромире. Но нам пора от "физических приложений" вновь вернуться к математическому содержанию музыкальной гаммы, которая таит в себе еще немало секретов.
С благодарностью к источнику: Библиотека по математике. Математика и искусство
The post «Космическая музыка»: от Платона до Кеплера first appeared on Математику в помощь.
]]>The post Учитесь решать задачи first appeared on Математику в помощь.
]]>В математике вы должны учиться многим важным умениям, играющим огромную роль в жизни каждого человека, в его работе: строить математические объекты, правильно определять понятия об этих объектах, устанавливать и доказывать существенные свойства этих понятий, проводить их классификацию. Но есть еще одно трудное, но важное умение, которому вам надо научиться,- это умение решать задачи.
Ведь с задачами (житейскими, производственными, научными) человек встречается ежедневно. Любое дело, любая работа в конечном счете сводится к решению задач. Поэтому научиться решать задачи чрезвычайно важно. Конечно, в математике решаются не любые задачи, а лишь математические и сводимые к ним. Но умение решать математические задачи оказывает огромное влияние на общее умение решать задачи, и тот, кто умеет решать эти задачи, сумеет решить и другие.
Поэтому учитесь, учитесь решать математические задачи!
Почему некоторые из вас не умеют самостоятельно решать задачи? Почему они не знают, как подступиться к решению новой незнакомой задачи?
Главная причина состоит в том, что эти ученики не понимают сущности задач, сущности их решения, не владеют общими методами поиска их решений.
Решение задач - это сложная работа. Материалом, над которым производится эта работа,- сами задачи, методы их решения - это инструменты для работы, а само решение - это процесс работы, процесс применения инструментов к материалу. Поэтому, чтобы облегчить решение задачи, надо, конечно, знать материал этой работы, т. е. сами задачи - как они устроены, из чего состоят, надо знать и владеть инструментами - методами решения задач, и научиться разумно применять эти инструменты.
Рассмотрим кратко основные особенности задач, решаемых в математике. В математике решаются собственно математические задачи, объектами которых являются какие-либо математические объекты, понятия и практические задачи, сводимые к математическим задачам, объектами которых являются реальные предметы или явления.
Примерами математических задач являются задачи на решение уравнений, неравенств, разные геометрические задачи и т. д. Примерами практических задач являются задачи, в которых речь идет о движении поездов, о работе, о размерах реальных предметов и т. д.
Для сведения практических задач к математическим реальные объекты, рассматриваемые в этих задачах, заменяются соответствующими математическими объектами (числами, отрезками, функциями и т. д.), и тем самым получается модель практической задачи - математическая задача. Приведем пример.
Задача 1. Велосипедист едет из одного города в другой со скоростью 10 км/ч. Если бы он ехал со скоростью 12 км/ч, то приехал бы в город на 4 ч раньше. Каково расстояние между городами?
Для решения этой задачи рассматриваемые в ней реальные объекты - расстояние между городами и скорости велосипедиста - заменяем соответственно математическими объектами - искомое х и числа 10 и 12. Тогда легко составить уравнение:
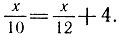
Это уравнение и есть модель данной задачи - соответствующая математическая задача.
Как устроены задачи? Из каких частей они состоят?
Всякая задача содержит одно или несколько условий - высказываний, принимаемых нами за истинные, и одно или несколько требований.
Задача 2.В круге проведены две взаимно перпендикулярные хорды, одна длиной 16 см, другая 14 см. Расстояния этих хорд до центра равны 1 см и 4 см. Определить отрезки, на которые делятся хорды точкой их пересечения.?
Построим указанные в задаче объекты: окружность центра О и две взаимно перпендикулярные хорды. Из центра О опустим на хорды перпендикуляры, чтобы найти их расстояние от центра (рис. 10). Тогда в этой задаче можно выделить следующие условия и требования:
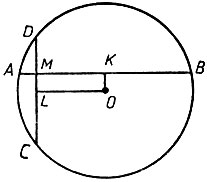
Рис. 10
Условия: 1) О - центр окружности; 2) АВ - хорда; 3) CD - хорда; 4)АВ⊥ CD; 5) АВ= 16; 6) CD= 14; 7) М - точка пересечения АВ и CD; 8) OK⊥AB; 9) ОK=1; 10) OL⊥OD; 11) OL = 4.
Требования: 1) найти AM; 2) найти ВМ; 3) найти СМ; 4)найти DM.
Как видим, эта простая задача содержит 11 условий и 4 требования. А как построены условия? Анализируя их, устанавливаем, что каждое условие содержит один или несколько объектов,которых идет речь в условиях. Так, в условии 1 имеется один объект - точка О, точно так же в условиях 2 и 3 по одному объекту - отрезки АВ и CD, а вот уже в условии 4 два объекта: отрезки АВ и CD, а в условии 7 даже три объекта: отрезки АВ и CD и точка М. По одному объекту содержат условия 5, 6, 9 и 11 и по два объекта условия 8 и 10.
Если в условии имеется один объект, то указывается его качественная или количественная характеристика. Так, в условии объект - точка О характеризуется как центр окружности, в условиях 2 и 3 - объекты - отрезки АВ и CD характеризуются как хорды. Это все качественные характеристики. В условии 5 дается количественная характеристика объекта - отрезка АВ, а именно указано, что его длина равна 16. Точно так же в условиях 9 и 11 указаны количественные характеристики рассматриваемых там объектов.
Если же в условии заданы два или более объекта, то указывается соотношение между ними. Так, в условии 4 два объекта - отрезки АВ и CD и в нем указано соотношение между ними: они взаимно перпендикулярны. В условии 7 соотношения между тремя ее объектами состоят в том, что один из них - точка М есть точка пересечения двух других объектов - отрезков АВ и CD и т. д.
Что касается требований, то в математических задачах наиболее часто встречаются такие виды требований: 1) найти искомое (величину, форму, отношение); 2) преобразовать заданный объект в другой вид; 3) построить некоторый объект с заданными характеристиками; 4) доказать справедливость некоторого утверждения.
В приведенной задаче 2 все четыре требования первого вида. Теперь рассмотрим, в чем состоит решение задачи.
Будем решать задачу 2.
- В четырехугольнике OKML углы L, К и М - прямые по построению, тогда и угол О также прямой, ибо сумма углов четырехугольника равна 360°.
- Следовательно, по определению прямоугольника этот четырехугольник OKML - прямоугольник.
- В прямоугольнике противоположные стороны равны, поэтому MK = OL, a OL по условию 11 равен 4, значит, и MK = 4 и т. д.
Как видим, решение задачи состоит из одного или нескольких шагов. Каждый шаг решения состоит в том, что мы применяем какое-то общее положение математики (определение, теорему, формулу, правило и др.) к условиям задачи или к полученным ранее результатам решения и выводим из этого следствие. Следствием последнего шага решения задачи должно быть то, что требуется в задаче.
Приведем еще один пример.
Задача 3. Разложить на множители многочлен х4 + 4 (1).
В этой задаче имеется одно условие: x4+ 4 - многочлен, и одно требование: преобразовать этот многочлен и представить его в виде произведения двух или нескольких многочленов. Это требование второго вида.
Решение этой задачи состоит из следующих шагов.
- Прибавим к данному многочлену (1) выражение 4x2-4x2, равное нулю, от этого значение (1) не изменится, получим:
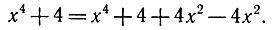 (2)
(2) - Сгруппируем члены (2) следующим образом:
Это мы имели право сделать на основе переместительного и сочетательного законов сложения.
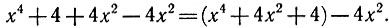 (3)
(3) - Применим к выражению, стоящему в скобках в правой части (3), формулу квадрата суммы, получим:
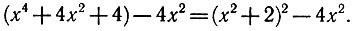 (4)
(4) - Представим 4x2 как (2x)2, тогда имеем:
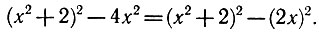 (5)
(5) - Применим к правой части (5) формулу разности квадратов:
Сопоставим все полученные равенства на основе аксиомы: если а = b и b = с, то а -с, получим окончательно:
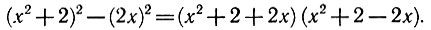 (6)
(6)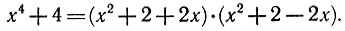 (7)
(7)
Это решение можно изобразить следующей схемой:?

Итак, решение любой задачи состоит в том, что находят такую последовательность общих положений математики, применяя которые к условиям задачи или к их следствиям в конечном итоге удовлетворяем требованиям задачи.
Наибольшая трудность в решении задачи - это нахождение указанной последовательности общих положений математики. Если эта последовательность уже найдена, то все остальные в решении - применение этих общих положений к условиям задачи или к следствиям, не представляет большого труда.
Для многих задач в самой математике разработаны эти последовательности общих положений, которые образуют известные общие правила (или, как говорят, алгоритмы) решения задач определенного вида.
Так, например, для производства всех действий над числом имеются готовые правила. Имеются особые правила и для решения многих алгебраических и геометрических задач. Однако большей частью эти правила сформулированы в математике в свернутом виде. Для того чтобы применить их для решения соответствующих задач, вы должны эти свернутые правила развернуть в пошаговую программу.
Например, формула (а+b)2 = а2 + 2аb +b2 есть правило для возвышения двучлена в квадрат. Для применения этого правила к решению какой-либо задачи надо это правило развернуть в пошаговую программу. Покажем, как это делается на примере решения задачи:
Представить в виде многочлена выражение (2х-3у)2

Математические задачи, для которых в математике имеются готовые правила - программы их решения, называются стандартными. Решение стандартных задач особых трудностей не представляет. Надо лишь распознать вид данной задачи, вспомнить соответствующее этому виду задач правило решения, развернуть это правило в пошаговую программу и применить ее к условиям данной задачи.
Значительно труднее решать нестандартные задачи, для которых в математике нет готовых правил. Решение нестандартных задач состоит в том, чтобы свести их к решению одной или нескольких стандартных задач. Например, задача 3 является нестандартной, но мы свели ее к решению нескольких стандартных задач. Приведем еще пример.
Задача 4. Построить трапецию, если даны большее основание, средняя линия и углы при меньшем основании.
Решение. В этой задаче дано (рис. 11):
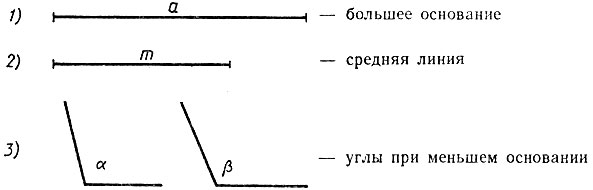
Рис.11
Требование задачи: построить трапецию по заданным элементам. Эта задача нестандартная, ибо в математике нет правила построения трапеции по указанным элементам.
Ищем способ решения.
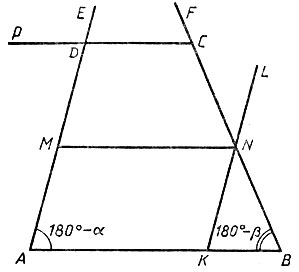
Рис.12
Пусть ABCD - искомая трапеция (рис. 12). Сразу построить всю трапецию или какую-либо ее часть, как видно, нельзя. Причина состоит в том, что заданные элементы разобщены. Так, заданные углы находятся не при известных большем основании или средней линии, а при неизвестном меньшем основании. Однако, зная углы при меньшем основании, легко найти и углы при большем основании: они дополняют соответствующие углы при Рис. 12 меньшем основании до 180°. Найдя их, мы тем самым установим направления боковых сторон трапеции в известных вершинах А и В большего основания. Теперь осталось найти положение средней линии. Для этого заметим, что NK||AM отсекает от АВ отрезок AK = MN. Следовательно, можно отложить на АВ отрезок АK, равный MN, и через точку К провести прямую, параллельную AD, до пересечения с ВС в точке N. Тем самым определится середина боковой стороны ВС. Отложив от N отрезок NC, равный BN, мы найдем вершину С, а проведя через нее прямую, параллельную АВ, найдем и последнюю вершину D.
Таким образом мы свели решение этой нестандартной задачи к решению следующих стандартных задач:
- На произвольной прямой отложить отрезок АВ = а.
- Построить угол, смежный с данным углом α; то же для угла β.
- Построить угол, равный смежному с α, так, чтобы его вершиной была точка А, а одной стороной - отрезок АВ, получаем угол ВАЕ; то же для угла, смежного с β, при вершине В и стороной ВА, получаем угол ABF.
- Отложить от А на прямой АВ отрезок АК=m.
- Провести через точку К прямую KL||AE.
- Найти точку пересечения прямой KL и BF, получаем точку N.
- Отложить от точки N на прямой BF отрезок NC = BN.
- Провести через точку С прямую СР||АВ.
- Найти точку пересечения прямых СР и АЕ, получаем точку D. Фигура ABCD - искомая трапеция.
Все шаги этого решения представляют собой стандартные задачи.
Конечно, надо еще доказать, что построенная фигура действительно есть искомая трапеция, установить условия, при которых задача имеет решения, но это сделать уже нетрудно.
При поиске способа решения нестандартных задач, при сведении их к стандартным надо пользоваться теми же эвристиками, которые мы указали в 8-й беседе. Но эти эвристики в данном случае лучше сформулировать несколько иначе, а именно:
1. Если можно, надо сложную задачу разбить на несколько более простых задач.
В рассмотренной выше задаче 4 мы разбили ее на 9 простых стандартных задач. Приведем еще один пример разбиения задачи на простые задачи.
Задача 5. Построить график функции:
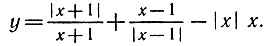 (1)
(1)
Решение. Сразу построить график этой функции вряд ли возможно. Попытаемся разбить эту задачу на части - более простые задачи, рассматривая заданную функцию в таких промежутках изменения х, в которых график функции легко по-строить. Так как в выражение (1) входят модули |x+1|, |х-1| и |x|, то естественно рассмотреть те промежутки, в которых значения этих модулей определенные. Очевидно, что для этого надо выделить точки, в которых эти модули меняют свое значение. Этими точками являются числа - 1, 1 и 0. Поэтому рассмотрим четыре промежутка: x< - 1, -1<x<0, 0<x<1 и x>1. Тем самым наша задача разбивается на 4 более простые задачи.
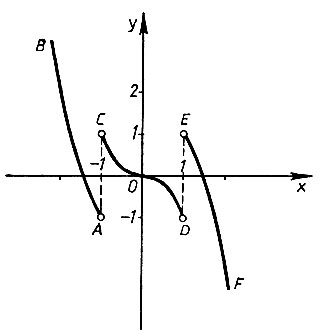
Рис.14
- Построить график функции (1) в промежутке x<-1.
В этом промежутке
График этой функции мы знаем, как строить, это будет часть параболы АВ (рис.13)
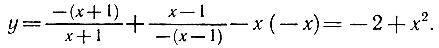
- Построить график функции (1) в промежутке -1<x≤0.
В этом промежутке
Графиком будет часть параболы ОС.
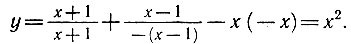
- Построить график функции (1) в 0<x<1.
В этом промежутке
Графиком будет часть параболы OD.
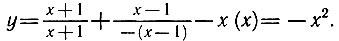
- Построить график функции (1) в промежутке x>1
В этом промежутке
Графиком будет часть параболы EF.
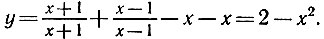
Таким образом мы полностью построили график функции (1), он состоит, как видим, из четырех частей.
В данном случае разбиение сложной задачи на части - более простые задачи, мы произвели, разбив область задачи на части. Иногда разбиение сложной задачи можно производить разбиением условий задачи на части, а иногда можно разбивать на части требование задачи. Вот пример такой задачи.
Задача 6. При каких значениях а оба корня уравнения х2-2ах+4 = 0 (1) положительны?
Решение. Для того чтобы оба корня (1) были положительны, нужно, во-первых, чтобы (1) имело два корня, а для этого, как известно, необходимо, чтобы дискриминант уравнения был неотрицательный. Во-вторых, так как свободный член (1) положительный, то оба корня имеют одинаковые знаки, а поэтому, чтобы они имели знаки "плюс", нужно, чтобы коэффициент среднего члена был отрицательный.
Следовательно, разбив требование задачи на указанные две части, мы разбиваем и саму задачу на две более простые задачи:
- При каких значениях а дискриминант уравнения (1) неотрицательный?
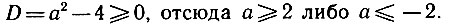 (2)
(2) - При каких значениях а коэффициент среднего члена уравнения (1) отрицательный?
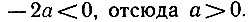 (3)
(3)
Сопоставляя (2) и (3), получаем окончательно: а≤2. При этих значениях а оба корня (1) будут положительны.
Если не видно, как решить задачу, то надо попытаться преобразовать ее или заменить другой, равносильной ей.
Приведем пример.
Задача 7. Решить систему уравнений
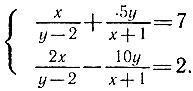
Решение. Проще всего эту систему решить, заменив ее другой с помощью подстановки:
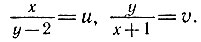 (1)
(1)
Тогда исходная система переходит в следующую, ей равносильную: 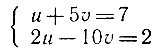 Решив эту систему, найдем:
Решив эту систему, найдем: 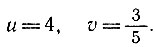 Подставив в (1), получаем новую систему:
Подставив в (1), получаем новую систему:
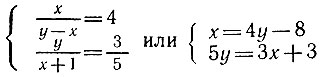
Решив эту систему, найдем окончательно:
Приведем еще один пример.
Задача 8. Расстояние между двумя колхозами 12 км. Колхозник вышел из своего колхоза в 9 ч 25 мин и прибыл в другой в 13 ч 15 мин. На следующий день он отправился в обратный путь в 11 ч и пришел домой в 14 ч 40 мин. На каком расстоянии от его колхоза находится пункт, который колхозник проходил в один и тот же час как на прямом, так и на обратном пути.
Решение. Обычный способ решения подобных задач - составление уравнения или системы уравнений - в данном случае трудно применить, ибо не видно, как составить уравнение; вопрос задачи уж очень необычный. Проще эту задачу решить, заменяя ее графической моделью.
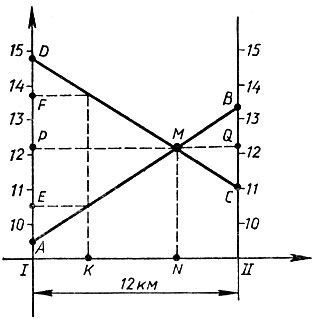
Рис. 14
Для этого в системе координат, где на оси абсцисс откладываем в каком-то произвольном масштабе расстояние, а на оси ординат - время в часах и минутах, притом за начало на оси времени берем не 0 ч, а 9 ч утра, строим графики движения колхозника туда и обратно (прямые АВ и CD) (рис. 14).
Если мы возьмем какой-либо пункт на пути колхозника, например пункт К, то этот пункт он проходил на прямом и обратном пути в разное время: на прямом пути в Е ч, а на обратном - в F ч. Но есть один пункт N, который он проходил в одно и то же время как на прямом, так и на обратном пути: этот пункт соответствует точке пересечения графиков его движения - точке М. Это и есть искомый пункт.
Чтобы найти расстояние этого пункта от первого колхоза, рассмотрим треугольники AMD и СМВ, они подобны. Поэтому их высоты МР и MQ пропорциональны сторонам AD и СВ. AD= 14 ч 40 мин - 9 ч 25 мин =5 ч 15 мин = 315 мин, СВ =13 ч 15 мин - 11 ч = 2 ч 15 мин = 135 мин. Получаем такую пропорцию: PM:MQ=315:135 = 7:3. Так как PM+MQ = PQ = 12 км, то находим, что РМ = (7/10)*12 км = 8,4 км.
3. Если данные и искомые (неизвестные) задачи прямо (явно) не связаны, то надо ввести вспомогательные элементы, которые их связывают.
Приведем пример использования этой эвристики.
Задача 9. Эту задачу придумал Исаак Ньютон (1643-1727).
Трава на лугу растет одинаково густо и быстро. Известно, что 70 коров съели бы всю траву на лугу за 24 дня, а 30 коров - за 60 дней. Сколько коров съедят всю траву на лугу за 96 дней?
Решение. Непосредственно составить уравнение или систему уравнений по данным задачи нельзя, ибо количество коров и число дней прямо не связаны: они не находятся в прямой или обратной пропорциональности. Чтобы найти связь между ними, введем вспомогательные элементы:
- первоначальное количество травы на лугу - а ед.
- каждый день там вырастает - b ед.
- одна корова за 1 день съедает - с ед.
Теперь можно составить такие уравнения: в первый раз всего травы за 24 дня выросло: а + 246, 70 коров за 24 дня съели 70*24с ед. травы. Тогда по условию a+ 246 = 70*24с. (1)
Аналогично получаем: а + 606 = 30 -60с (2)
а+ 966 = x*96с, где x - искомое (3) количество коров.
Вычитая из (2) почленно (1), найдем: 366 = 120с или с = 0,36. (4) Подставляя значение с из (4) в (1), найдем: а = 4806. (5)
Подставим значения а и с из (5) и (4) в (3), получим: 576b = 28,8*x*b. Так как b≠0, то, сократив на b, найдем: x = 20 (коров).
Конечно, при решении многих нестандартных задач приходится использовать не одно какое-либо эвристическое правило, а несколько. Знание этих эвристик, владение ими очень помогает при поиске решения нестандартных задач.
Итак, вам надо научиться решать задачи, математические и практические. Для этого прежде всего надо очень внимательно их изучать, анализировать, устанавливать каждый раз условия и требования, содержащиеся в задаче, выяснять, какие объекты, их характеристики и отношения входят в условия, что означают требования задачи. На такой подробный и тщательный анализ не надо жалеть ни времени, ни сил. Только на основе такого анализа будет эффективен ваш поиск способов решения задач. При этом следует помнить, что решение задачи сводится к нахождению таких общих положений математики, применяя которые к условиям задачи или к их следствиям можно удовлетворить ее требования. Поэтому общие положения математики: ее аксиомы, теоремы, правила, формулы, тождества надо знать, надо помнить. Без такого знания вы не сумеете решать задачи.
Нахождение способа решения задачи подобно изобретению, а изобретение требует воображения, догадки, фантазии. Поэтому развивайте у себя эти качества.
А главное - не спешите при решении задач, не стремитесь решить как можно больше задач. Лучше решить меньше задач, но вдумчиво, с пользой. А для этого, решив задачу, обдумайте проделанное решение, установите, в чем своеобразие задачи, ее решения, что нового вы узнали и приобрели, решив эту задачу. Вот это новое, вот те общие и специальные приемы, которые вы использовали при решении этой задачи, постарайтесь запомнить, усвоить. Все это вам пригодится при решении других задач.
8.1. Проанализируйте следующие задачи, выделите в каждой из них все условия, установите, какие объекты входят в каждое условие, какие характеристики или отношения между объектами заданы в этих условиях.
а) Путешественник проехал автобусом и по железной дороге всего 600 км, причем автобусом он проехал в 4 раза меньше, чем по железной дороге. Сколько часов был в пути путешественник, если автобусом он проезжал 30 км в час, а по железной дороге 32 км в час?
б) Равнобочная трапеция с боковой стороной, равной 15 см, и углом при большем основании 60° описана около круга. Найти основания трапеции.
8. Выясните, какие условия и какие требования содержат следующие задачи:
а) Какая из трех высот равнобедренного треугольника может быть больше его основания?
б) Что больше и на сколько: частное (x4-3x2+1):(x2-x-1) или произведение (x-10)*(x+11)?
8.3. Напишите пошаговую программу решения следующей задачи, указывая для каждого шага общие положения математики, на основе которых выполняется решение:
Решить неравенство: 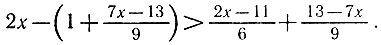
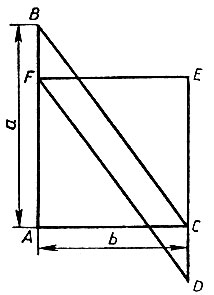
Рис. 15
8.4. Решите следующие задачи и установите, какие эвристические правила вы при этом использовали:
а) Через одну из вершин треугольника проведена вне его прямая MN. Зная, что расстояния от других вершин треугольника до прямой MN равны 10 см и 8 см, найти расстояние середин сторон треугольника до прямой MN.
б) Построить треугольник по двум высотам и медиане к третьей стороне.
в) Найти сумму площадей квадрата ACEF и параллелограмма FBCD (рис. 15), если АВ = а и АС=b.
г) Решить уравнение: x12-x9+x8-x5+1=0.
д) Поезд проходит расстояние от A до В за 10 ч 40 мин. Если бы скорость поезда была бы на 10 км/ч меньше, то он пришел бы в В на 2 ч 8 мин позже. Определить расстояние между А и В.
е) На берегу круглого озера четыре пристани K, L, Р и Q. От пристани К отплывает катер, а от пристани L одновременно отплывает лодка. Если катер поплывет прямо в Р, а лодка - прямо в Q, то они встретятся в некоторой точке X озера. Доказать, что если катер поплывет в Q, а лодка в Р, то они достигнут этих пристаней одновременно.
С благодарностью к источнику: Библиотека по математике. Учитесь учиться математике
The post Учитесь решать задачи first appeared on Математику в помощь.
]]>The post Математика ум в порядок приводит first appeared on Математику в помощь.
]]>Дело в том, что наше мышление, перерабатывая ощущения, восприятия и представления о предметах и явлениях, как бы предвосхищает будущее, указывает нам, как поступить, что сделать в создавшейся ситуации. Поэтому от того, как "работает" наше мышление, зависит, поступим ли мы правильно и разумно или нет.
Человек рождается без умения мыслить, лишь с задатками к нему. Мыслить он научается постепенно в процессе жизненной практики, в общении со взрослыми и своими сверстниками, и особенно в обучении.
Одним из наиболее важных качеств мышления является его логичность т. е. способность делать из правильных посылок (суждений, утверждений) правильные выводы, находить правильные следствия из имеющихся фактов.
О человеке, у которого хорошо развито логическое мышление, говорят, что он основательно мыслит, дисциплинированно рассуждает. Такой человек, как правило, не допускает ошибок в своих рассуждениях и выводах. Хорошо развитое логическое мышление предостерегает человека от промахов и ошибок в практической деятельности. И вот оказывается, что это ценнейшее качество возникает и развивается главным образом в процессе изучения математики, ибо математика - это практическая логика, в ней каждое новое положение получается с помощью строго обоснованных рассуждений на основе ранее известных положений, т. е. строго доказывается. Ломоносов приведенными выше словами и имел все это в виду. На это же значение изучения математики указывал М. И. Калинин, призывая молодежь серьезно изучать математику: "Математика дисциплинирует ум, приучает к логическому мышлению. Недаром говорят, что математика - это гимнастика ума".
В связи с этим легко понять, почему так важно самому выводить формулы, доказывать тождества и теоремы. Ведь дело не в том, чтобы вы запомнили их на всю жизнь. Возможно, что они забудутся, но останется привычка рассуждать, сохранится умение объяснять, доказывать не только другим, но и самому себе какие-то истины, укрепится умение искать и находить рациональные пути решения возникающих в жизни проблем.
Вот эту культуру, дисциплину мысли, ее последовательность и доказательность, глубину и критичность, широту и оригинальность, а также необходимую пищу для мышления - систему знаний - нам дает школа, и в частности уроки математики. Эта сторона обучения математике особенно важна в наши дни, поскольку сейчас объем необходимых для человека знаний резко и быстро возрастает, поэтому необходимо каждому научиться самостоятельно пополнять свои знания. Овладеть этими умениями вам поможет добросовестное самостоятельное изучение математики.
Изучение математики формирует не только логическое мышление, но и много других качеств человека: сообразительность, настойчивость, аккуратность, критичность и т. д.
Очень важным среди них является пространственное воображение, т. е. умение представить в уме (вообразить) какие-то предметы, фигуры и при этом увидеть их не только неподвижными, но и в изменении, т. е. представить, что произойдет, если их как-то переместить, повернуть и т. д. При изучении математики, при решении геометрических задач вам все время приходится делать это, и тем самым у вас постепенно развивается эта важная способность. Почему важная? Поясним на примерах. Токарь, получив чертеж, должен до работы представить себе образ той детали, которую ему нужно выточить. А портниха должна обладать хорошими способностями к пространственному воображению, чтобы правильно раскроить материал. Эти же умения и способности позволяют шахматисту направлять фигуры на доске, а полководцу - войска на поле боя. Художник или писатель должен уметь детально вообразить ту ситуацию, которую он хочет описать. Высокий уровень ориентировки в пространстве является необходимым условием для спортсмена, позволяющим ему овладеть своим телом. А инженер? А оператор? А космонавт?... Нет такой области человеческой деятельности, где не нужны были бы хорошие умения и способности к пространственному воображению.
Эта же способность представить в уме - вообразить - важна и для планирования своей работы, своих действий с. тем, чтобы они были наиболее разумными, рациональными и безошибочными.
Изучение математики, решение математических задач развивают, помимо пространственного воображения, и способность догадываться, угадывать заранее результат, способность разумно искать правильный путь в самых запутанных условиях. Прочтя задачу и еще не производя никаких действий, вы уже научились сразу видеть, что тот или иной способ непригоден для ее решения, а вот какой-то другой способ может быть использован.
Как видим, математику следует глубоко и серьезно изучать не только потому, что она служит основой научного познания, не только потому, что без нее нельзя сделать ни шагу в жизни, в практической деятельности на любой работе, но и потому, что процесс ее изучения способствует развитию у человека важнейших качеств и способностей.
Поэтому хотя изучение математики и требует большого и упорного труда, но оно приносит так много пользы, столь много радостей познания и преодоления трудностей, что вы никогда не пожалеете о затраченных усилиях.
Задание
Попытайтесь самостоятельно ответить на вопросы и решить задачи, приведенные ниже. Если вы это не сможете сделать, то прочтите указания или ответы, которые приведены в конце статьи, и попробуйте еще раз самостоятельно выполнить заданные упражнения. Если и после этого вы не сумеете это сделать, то постарайтесь разобраться коллективно или обратитесь за консультацией к учителю.
1. Почему стол на трех ножках на любом полу стоит не шатаясь, а стол на четырех ножках весьма часто шатается?
2. Портной, для того чтобы проверить, является ли лоскут материала квадратом, перегибал его по диагонали и смотрел, совпадают ли при этом вершины лоскута. Достаточна ли такая проверка? Почему?
3. Где, в каких науках используется декартова система координат?
4. Возьмите учебник физики. Проверьте, сумеете ли вы понять его содержание, если вдруг забудете всю математику.
5. Найдите в учебнике истории те страницы, на которых излагается изучаемая вами сейчас тема. Есть ли там математика?
6. Вспомните определение модуля числа. Пусть числу x: на координатной прямой соответствует точка X. Каков геометрический смысл выражения |х- 2|? Истолкуйте с этой точки зрения уравнение |х-2|+|х - 5|=а. Сообразите, при каких значениях а это уравнение не имеет решений. А при каких значениях а оно имеет бесконечное множество решений?
7. Докажите, что четных натуральных чисел столько же, сколько и нечетных.
8. Числа, кратные 10, очевидно, составляют лишь часть всех натуральных чисел. Между тем вам, должно быть, не трудно доказать, что их не меньше, а столько же, сколько всех натуральных чисел. В чем причина такого парадоксального (необычного) положения?
С благодарностью к источнику: Библиотека по математике. Учитесь учиться математике
The post Математика ум в порядок приводит first appeared on Математику в помощь.
]]>The post Математика и изучение реального мира first appeared on Математику в помощь.
]]>На протяжении нескольких веков физика и астрономия были основными источниками математических проблем и основными областями, в которых испытывалась сила новых математических методов. Однако в последнее время это положение вещей существенно изменилось. Сейчас, буквально на наших глазах, математические методы быстро входят в экономику, социологию, лингвистику, биологию и т. д. Возникли и вошли в обиход такие термины, как математическая лингвистика, математическая экономика, математическая биология. Чем же обусловлено такое энергичное вторжение математики в области, бывшие еще сравнительно недавно достаточно далекими от нее?
Было бы ошибкой считать, что важность точных количественных методов для таких наук, как биология, была понята лишь в наше время. На самом деле, первые попытки в этом направлении относятся к достаточно далекому прошлому. Так, например, еще в 1680 г. Джованни Борелли опубликовал в Риме обширный труд «О движении животных» (De Motu Animalium), в котором сделал попытку применить геометрические и механические соображения к исследованию движений животных и человека. Впрочем, первые идеи такого рода были, видимо, у Леонардо да Винчи - одного из самых универсальных гениев в истории человеческой культуры.
Переходя к более поздним временам, следует прежде всего упомянуть исследования Гельмгольца, который в своих работах по слуху и зрению пользовался математическим аппаратом, развитым в значительной мере им самим для изучения волновых процессов. Возможность изложить и исследовать биологические проблемы в физических и математических понятиях глубоко интересовала и немецкого физиолога прошлого века Дюбуа-Реймона.
Среди работ, относящихся к нашему столетию, следует прежде всего упомянуть фундаментальный труд д’Арси Томсона «О росте и форме» (1917 г.), посвященный применению математических методов к исследованию геометрических форм и процесса роста животных и растительных организмов. Несколькими годами позже была опубликована работа А. Лотка «Элементы физической биологии» (1924 г.), в которой автор, используя в основном аппарат теории дифференциальных и интегральных уравнений, рассматривает чрезвычайно широкий круг проблем - от молекулярных процессов в клетках до психических функций центральной нервной системы. Примерно к тому же времени относятся исследования итальянского математика В. Вольтерра, изложенные затем в его книге «Лекции по математической теории борьбы за существование» (1931 г.), и книга Дж. Холдейна «Математическая теория естественного отбора» (1924 г.). Начиная с 30-х годов число работ, содержащих попытки математического подхода к тем или иным проблемам биологии, стало быстро возрастать. Сложились целые коллективы, работающие в этом направлении (например, школа Н. Рашевского в США). Ряд важных идей, по существу предвосхитивших в известной мере исходные положения современной биокибернетики, содержится в исследованиях нашего соотечественника академика И. И. Шмальгаузена, начатых им еще в 30-х годах.
Среди различных математических методов уже сравнительно давно «завоевала права гражданства» в биологических исследованиях математическая статистика. Биологическими применениями статистических методов интересовался знаменитый английский статистик К. Пирсон. Более того, ряд исследований в области математической статистики, например работы Р. Фишера и его школы, в значительной мере стимулировались именно потребностями биологии.
Сущность математического подхода к изучению реального мира. Модели
Приведенный краткий и весьма неполный перечень работ, связанных с применением математических методов к биологическим проблемам, показывает, что такого рода исследования уже имеют довольно длительную историю. И все же о действительно широком проникновении математических методов в биологию стало возможным говорить лишь в самое последнее время. Впрочем, и сейчас еще эти методы в биологии играют гораздо меньшую роль, чем, скажем, в физике. Оказалось, что применять математику для исследования живой природы гораздо труднее, чем, например, для изучения движения планет. Для того чтобы понять природу этих трудностей, посмотрим, в чем же, собственно, состоит сущность математического подхода к изучению объектов и явлений окружающего нас мира.
Характерная черта математики состоит в том, что она оперирует, как правило, отвлеченными, идеализированными понятиями. Такие понятия, как, например, «прямая плоскость», «число», не означают каких-либо реальных предметов, а лишь некоторые «мысленные модели» существующих в природе вещей. К такого рода моделированию (моделированию в указанном здесь логическом смысле, а не в инженерном) приходится прибегать, по существу, всякий раз, когда речь идет о применении математики к изучению окружающего мира. Например, в механике мы вводим такие понятия, как «материальная точка», «идеальная жидкость» и т. д. Это тоже математические идеализации, т. е. модели реальных физических тел. А затем к изучению этих моделей применяется соответствующий математический аппарат, скажем, теория дифференциальных уравнений или что-либо еще.
Мы привыкли к делению наук на естественные и гуманитарные. При этом математику относят к естественным наукам в самую первую очередь. Но это не вполне справедливо. Скорее, математика занимает некое промежуточное положение, будучи связана с изучением как окружающей природы, так и различных форм человеческой деятельности. Можно сказать, что математика - это язык, на котором можно описывать различные явления. Но этот язык подчинен весьма жестким и строгим правилам логики. И научиться говорить на математическом языке о том или ином круге событий подчас весьма сложно. Мы лучше всего умеем говорить на нем о механических и физических явлениях, но в принципе этот язык чрезвычайно универсален.
Что мы умеем моделировать
Когда строится та или иная модель, то она, конечно, должна прежде всего отражать существенные черты моделируемого объекта, иначе ее изучение мало что нам даст для познания этого объекта. С другой стороны, модель не должна быть слишком сложна, иначе она будет недоступна для точного математического исследования*. Если речь идет о моделировании сложной системы, то весьма трудно удовлетворить одновременно обоим этим требованиям - достаточная простота и, вместе с тем, достаточная «похожесть». Поэтому в первую очередь математические методы развивались применительно к изучению достаточно простых систем. Примером области естествознания, в которой математические методы применяются давно и с большим успехом, может служить классическая механика, в частности небесная механика. Развитые здесь математические методы позволяют весьма точно описывать движение системы материальных тел, например, предсказывать на много лет вперед солнечные и лунные затмения, вычислять орбиты комет и т. д. Однако и здесь возникает много трудных и сложных математических проблем**, в том числе и таких, которые остаются нерешенными до сих пор, несмотря на то, что рассматривается такая система как система материальных точек.
* (Говорят, что однажды Микеланджело, отвечая на вопрос о том, как создать скульптуру из глыбы камня, сказал: «Скульптура уже заключена в камне. Нужно только срезать все лишнее, и она предстанет перед вами». Эти слова можно применить и к тому, как создается абстрактная модель реального явления. Но как отделить «лишнее» от «необходимого»?. Это трудно и в искусстве и в науке.)
** ( Примером здесь может служить известная задача трех тел, состоящая в определении всех возможных движений трех масс, связанных силами взаимного притяжения.)
Что же касается любой биологической системы, то построение ее удовлетворительной математической модели оказывается, как правило, чрезвычайно сложным делом.
Появление новых возможностей
Итак, математические методы исследования мы можем успешно развивать в тех областях, где нам удается создать достаточно хорошие общие понятия, создать соответствующий изучаемым явлениям «математический язык». Если явления, которые мы изучаем, сложны, то они могут оказаться за пределами возможностей тех математических методов, которыми мы располагаем.
Однако сейчас у нас есть серьезные основания для того, чтобы смотреть на дело оптимистически. За последние 20-25 лет в самой математике произошли существенные изменения, значительно расширившие круг ее возможностей. Часто это расширение области применимости математических методов, происшедшее в последние годы, связывают в первую очередь с появлением быстродействующих вычислительных машин. Бесспорно, появление таких машин сыграло тут очень большую роль, но дело не только в них. На протяжении тех же 20-25 лет, в которые укладывается вся история развития электронной вычислительной техники, в математике возник ряд новых направлений и областей, связанных именно с исследованием сложных систем и анализом таких ситуаций, в которых классические математические методы неприменимы. К таким областям математики относятся теория игр, теория автоматов, новые методы решения задач об оптимальном регулировании, теория операций и т. д. возможно, конечно, что людям во все времена было свойственно переоценивать научные достижения именно своей эпохи, однако, даже сделав известную скидку на это обстоятельство, можно утверждать, что именно сейчас математика гораздо больше приспособлена к анализу сложных систем, имеющих много степеней свободы и состоящих из большого числа взаимодействующих между собой частей, чем это было еще сравнительно недавно, скажем, в первой половине нашего века.
Сейчас выяснилась возможность построения достаточно удовлетворительных математических моделей в таких сложных и запутанных ситуациях, которые возникают, например, в экономике. Интересным примером возникновения хорошей математической модели в области, в которой это трудно было ожидать заранее, может служить теория информации. Хотя она возникла всего около 20 лет тому назад, сейчас она представляет собой развитую математическую теорию, со многими теоремами и разнообразными методами. Однако основной и решающий шаг в построении теории, сделанный основоположником этой теории К. Шенноном в конце 40-х годов, состоял не в теоремах, а в формулировке таких фундаментальных понятий, как количество информации и пропускная способность канала, т. е. в создании такой модели, которая отражает общую математическую сущность самых разнообразных способов передачи сообщений.
С благодарностью к источнику: Библиотека по математике. Математика в биологии
The post Математика и изучение реального мира first appeared on Математику в помощь.
]]>The post Мировая гармония first appeared on Математику в помощь.
]]>Рано или поздно всякая правильная
математическая идея находила
применение в том или ином деле.
Алексей Николаевич Крылов

Геометрические мозаика
"Симметрия... охватывает свойства всех физических полей, с которыми имеют дело физик и химик",- считал академик Владимир Иванович Вернадский. Но если уж речь идет о физике и химике, то что говорить о математике?
Правильные геометрические мозаики, истинные образцы симметрии, как мы имели удовольствие убедиться, двойственны в том смысле, что центры составляющих их фигур служат вершинами для других фигур. И точно так же дело обстоит у правильных многогранников, только их в этом случае называют взаимными. Октаэдр, например, взаимен кубу* (Рис. 20, Рис. 21), икосаэдр - додекаэдру (Рис. 22), а вот тетраэдр взаимен сам себе (Рис. 23), как квадратная мозаика тоже сама себе двойственна. Об этом говорит и симметрия символов Шлефли - {4,3} и {3,4} у куба и октаэдра, {3,5} и {5,3} - у икосаэдра и додекаэдра, {3,3} - у тетраэдра и {4,4} - у квадратной мозаики. Именно поэтому родственные мозаики и многогранники изящнейшим образом вписываются друг в друга.
 Рис. 20 |
 Рис. 21 |
 Рис. 22 |
 Рис. 23 |
* ("Среди правильных тел самое первое, начало и родитель остальных - куб, а его, если позволительно так сказать, супруга - октаэдр, ибо у октаэдра столько углов, сколько у куба граней, а центры граней куба соответствуют вершинам октаэдра",- писал Кеплер. Это видно и на гравюре Эсхера "Кристалл".)
Но вот что настораживает. Два тетраэдра, прошедших один сквозь другой, образуют восьмигранник - вы увидите его в правом верхнем углу гравюры Маурица Эсхера "Звезды"*.
* (На этой же гравюре внимательный глаз различит и все правильные многогранники. В частности, нижний хамелеон держится передкими лапами за октаэдр и тетраэдр, а хвостом обвил другой октаэдр. Верхняя же тварь, наоборот, обвила хвостом ребро тетраэдра, а лапами вцепилась в два октаэдра.)
Эта фигура встретится нам в виде гравюры "Двойной планетоид". Лука Пачоли, первым обнаруживший эту фигуру, назвал ее "продолженным октаэдром", а его великий друг Леонардо да Винчи сделал соответствующий деревянный каркас, перерисовав его затем в их общую книгу "О божественной пропорции". "Octacedron elevatus solidus", то есть "продолженный октаэдр сплошной",- написано там его рукой (Рис. 24). Иоганн Кеплер переоткрыл эту фигуру сто лет спустя и присвоил ей имя "стелла октангула" - "восьмиугольная звезда". Она встречается и в природе: это так называемый двойной кристалл. Но она же перечеркивает все, что было сказано до сих пор! Мы вынуждены признать "стеллу октангулу" правильным многогранником: ведь все ее грани - правильные треугольники одинакового размера и все углы между ними равны!replica high end watchesfind more informationdiscover here

Рис. 24
Что же это - шестое платоново тело?! Нет, просто удавшаяся провокация. В определении правильного многогранника сознательно - в расчете на кажущуюся очевидность - не было расшифровано слово "выпуклый". А оно означает дополнительное требование: "и все грани которого лежат по одну сторону от плоскости, проходящей через любую из них". Если же отказаться от такого ограничения, то к Платоновым телам, кроме "продолженного октаэдра", придется добавить еще четыре многогранника (их называют телами Кеплера-Пуансо), каждый из которых будет "почти правильным". Все они получаются "озвездыванием" Платонова тела, то есть продлением его граней до пересечения друг с другом, и потому называются звездчатыми. Куб и тетраэдр не порождают новых фигур - грани их, сколько ни продолжай, не пересекаются. Если же продлить все грани октаэдра до пересечения их друг с другом, то получится та же знакомая нам фигура, что возникает при взаимопроникновении двух тетраэдров - "стелла октангула", которую совсем недаром Лука Пачоли называл "продолженным октаэдром". Икосаэдр и додекаэдр дарят миру сразу четыре "почти правильных многогранника. Один из них - малый звездчатый додекаэдр (Рис. 25), полученный впервые Иоганном Кеплером, вы видите на эсхеровских гравюрах "Силы гравитации" и "Порядок и хаос".

Рис. 25
"Я недавно встретил человека, который сказал мне, что не верит даже в существование минус единицы, так как из этого следует существование квадратного корня из нее",- рассказывал Э. Ч. Титчмарш, современный английский историк математики. Подобная же история случилась и с кеплеровским звездчатым додекаэдром.
Открыв этот "колючий" многогранник, Кеплер так и назвал его "еж" и поместил в свою удивительную по фантастичности идей книгу "Мировая гармония", где космогонические и астрономические вопросы решались с помощью соотношений, найденных в музыке и в формах правильных многогранников и многоугольников*. Но ученые отказывались считать кеплеровского ежа многогранником.
* (Полное название этой книги, вышедшей в 1619 году,- "О гармонии мира пять книг". Разными авторами оно переводится как "Гармония мира" и как "О гармонии мира".)
У этого упрямства была своя логика и своя предыстория. Столетиями математики не признавали за всякого рода звездами права называться многоугольниками из-за того, что стороны их пересекаются. А тут - геометрическое тело, гранями которого служат пятиконечные звезды, да еще вдобавок пересекающиеся! Какой же это многогранник?! Людвиг Шлефли, который был уже настолько свободомыслен - все-таки XIX век!- что не изгонял геометрическое тело из семейства многогранников только за то, что его грани самопересекаются, тем не менее оставался непреклонным, как только речь заходила про малый звездчатый додекаэдр. Довод его был прост и весом: это кеплеровское животное не подчиняется формуле Эйлера! Его колючки образованы двенадцатью гранями, тридцатью ребрами и двенадцатью вершинами, и, следовательно, В+Г-Р вовсе не равняется двойке.
Шлефли был и прав, и не прав. Конечно же, геометрический ежик не настолько уж колюч, чтобы восстать против непогрешимой формулы. Надо только не считать, что он образован двенадцатью пересекающимися звездчатыми гранями, а взглянуть на него как на простое, честное геометрическое тело, составленное из 60 треугольников, имеющее 90 ребер и 32 вершины*.
* (На каждой из двенадцати пятиугольных граней "обычного" Додекаэдра возводится по пирамиде, следовательно, всего граней становится 5*12 = 60. Каждая пирамида добавит додекаэдру по пять ребер - всего их станет 30+(5*12) = 90. И, наконец, любая пирамида увенчана вершиной, поэтому к двадцати вершинам додекаэдра добавится еще двенадцать, итого 32. Все это хорошо видно на гравюре "Силы гравитации".)
Тогда В+Г-Р = 32+60-90 равно, как и положено, 2. Но зато тогда к этому многограннику неприменимо слово "правильный" - ведь грани его теперь не равносторонние, а всего лишь равнобедренные треугольники.
Красоте малого звездчатого додекаэдра находится на удивление мало места в нашей жизни: он служит разве что светильником, да и то очень редко. Даже изготовители елочных украшений и то не додумались сделать трехмерную звезду, а ею как раз и оказался бы этот многогранник.
И при том его еще и не надо было бы золотить - во всяком случае для геометров: золотое отношение, "божественная" пропорция связывает любой "брусок" каркаса обычного додекаэдра с тем же "бруском", но продолженным до точки встречи в вершине "колючки" кеплеровского ежа. Но Кеплер не додумался, что у полученной им фигуры есть двойник. Это увидел наш старый знакомый Август Фердинанд Мёбиус, а сам многогранник - он называется "большой додекаэдр" - построил французский геометр Луи Пуансо спустя без малого двести лет после кеплеровских звездчатых фигур. Если эти две удивительно красивые фигуры расположить рядом, то станет видна их "взаимность" (Рис. 25, Рис. 26).
Рис. 26
О двух других телах Кеплера-Пуансо (большом звездчатом додекаэдре - Рис. 27 и большом икосаэдре - Рис. 28) тоже можно было бы сказать немало интересного. Но, может быть, лучше просто полюбоваться на них и подумать: ведь удивительное дело, почему и в этой паре, "увидев" одну фигуру, Кеплер честь открытия второй оставил Пуансо?
 Рис. 27 |
 Рис. 28 |
А теперь, для отдыха глаз и души, еще раз взгляните на гравюру Маурица Эсхера "Порядок и хаос". Вот что пишет о ней сам художник: "Звездчатый додекаэдр, символ математической красоты и порядка, окружен прозрачной сферой. В ней отражена бессмысленная коллекция бесполезных вещей". Мы уже воспользовались одной из них - веревкой, когда говорили о головоломке сэра Уильяма Гамильтона. Тогда же нам понадобился и сам додекаэдр, но только не звездчатый, а обыкновенный - мы позаимствовали его с другой гравюры того же автора - "Рептилии". Посмотрите на нее внимательно, и вам представится случай полюбоваться еще одной мозаикой, составленной на этот раз из одних крокодилов, поверх которой наложена обычная, шестигранная.
"В мире нет места для некрасивой математики",- считал Готфрид Харди.
Обложку прекрасной книги Гарольда Скотта Макдональда Коксетера "Введение в геометрию" (ей тоже очень многим обязана эта "Рапсодия") украшает фигура, которую вычертил в 1932 году Джон Флаундере Петри, сын великого египтолога и - что гораздо интереснее - один из очень немногих людей на Земле, кто умел строить в своем воображении четырехмерные тела, подсчитывать в уме число их элементов и отчетливо представлять себе их взаимное расположение. Вычерченная им фигура, о которой идет речь, вполне земная, трехмерная, но и она была получена довольно непросто. Вписанный в сферу правильный икосаэдр спроецировали на эту сферу из ее центра (Рис. 29). Все его ребра перешли в дуги большого круга, которые разбили сферу на множество сферических треугольников. (Дуги эти на плоскости изображаются эллипсами, в этом и была основная сложность вычерчивания "фигуры Петри".) Таким образом, правильный многогранник породил правильную сферическую мозаику - узор, покрывающий всю сферу, составленный из одинаковых фигур. (Центральные и периферийные треугольники выглядят разными только из-за того, что спроецированный на сферу икосаэдр пришлось спроецировать еще раз - на плоскость страницы этой книги, а при этом нельзя обойтись без искажений.)

Рис. 29
Но у "фигуры Петри" есть еще одно замечательное свойство. Вглядитесь в нее повнимательнее, она того вполне заслуживает. Можно не только получить сеть сферических треугольников из правильного многогранника, но и, наоборот, этой сетью поймать платоново тело, да не одно, а целых два! Шесть треугольников, окружающих вершину, образуют треугольную грань раздувшегося до сферы икосаэдра, а десять треугольников, объединившихся вокруг вершины в центре,- пятиугольную грань такого же додекаэдра. Другие грани вы теперь увидите без труда. И, повинуясь вашей воле, разбитая на черно-белые треугольники сфера, подобно оборотню зрительных иллюзий, преобразуется то в двенадцати, а то и в двадцатигранник. Ничего удивительного в подобной двойственности нет, стоит лишь, вспомнить, что символ Шлефли у икосаэдра {3,5}, а у додекаэдра - {5,3}. То есть они взаимные многогранники: середины граней одного служат вершинами для другого (Рис. 22).
"Теория многогранников, в частности выпуклых многогранников,- одна из самых увлекательных глав геометрии" - таково мнение Л. А. Люстерника, члена-корреспондента Академии наук СССР, ученого, много сделавшего именно в этой области математики. Не будем же лишать себя удовольствия познакомиться с еще одним - самым многочисленным - отрядом многогранников, имеющих отношение к нашим Платоновым телам. Для этого надо лишь быть последовательным - отказаться еще от одного ограничения.
Почему правильные многоугольники, служащие гранями, так уж обязательно должны быть все на одно лицо? И сразу же обретают право на жизнь полуправильные многогранники, описанные еще Архимедом. Они получаются из Платоновых тел либо "отсечением углов", либо "отсечением ребер". Интересно, что две тысячи лет считалось, что архимедовых тел всего тринадцать, и лишь в 1957 году обнаружилось, что верхнюю часть ромбокубооктаэдра, состоящую из пяти квадратов и четырех правильных треугольников, можно повернуть на 45 градусов. Так появился четырнадцатый полуправильный многогранник, который можно было бы назвать ашкинузеэдром - в честь открывшего его советского математика В. Г. Ашкинузе.
Итак, к пяти правильным Платоновым и пяти почти правильным, то есть звездчатым, телам Кеплера-Пуансо надо прибавить еще четырнадцать полуправильных тел Архимеда-Ашкинузе. Но тогда уж, по справедливости, надо включить в этот реестр и "почти полуправильные", то есть звездчатые полуправильные многогранники: например, звездчатый кубооктаэдр, изображенный на гравюре М. К. Эсхера "Кристалл". Тут, однако, есть одна тонкость. Если про правильные - обычные и звездчатые- многогранники Огюстен Коши в 1812 году строго доказал, что их может быть только десять, то касательно полуправильных известно лишь, что 14 обычных дают 51 звездчатый. Но исчерпывается ли этим "полуправильное многообразие" - этого сегодняшние геометры не знают*.
* (Множество звездчатых тел получил советский исследователь В. Н. Гамаюнов. Фигуры эти, обладающие своеобразной красотой, легли в основу нескольких архитектурных проектов" созданных В. А. Сомовым и А. М. Бреславцем.)
Впрочем, даже если и удастся доказать, что эти фигуры заполняют собой всю "обойму", то и тогда никто не назовет суммарного числа полуправильных фигур. Ведь в их число входят еще две бесконечные серии, описанные Архимедом в трактате "О многогранниках". Это призмы и антипризмы - фигуры, в основаниях которых лежат любые правильные n-угольники, а боковыми гранями служат либо квадраты, либо равносторонние треугольники. Так, словно потешаясь над нашим вполне естественным стремлением провести полную инвентаризацию всех ее тайн, Природа приготовила для нас целых две геометрические бесконечности.
Но это не единственная из ее геометрических шуток.
"Изо всех двухсот миллиардов мужчин, женщин и детей, которые когда-либо прошли по влажному песку с сотворения мира до собрания британской ассоциации в абердине в 1885 году, сколько найдется таких, которые на вопрос "сжался ли песок под вашей ногой?" ответили бы иначе, чем "да!"?"- вопрошал на лекции в Балтиморе лорд Кельвин. И на самом деле, никто не усомнился бы в правильности такого ответа, пока Осборн Рейнольде не доложил в Абердине о своих наблюдениях и выводах. "Когда нога надавливает на песок, плотный после ушедшего прилива, участок, находящийся вокруг ноги, тотчас же становился сухим,- рассказывал он членам Британской ассоциации ученых.- Надавливание ноги расплющивает, расширяет песок, и чем сильнее оно, тем больше воды выдавливается из этого места в окружающее пространство... Поднимая ногу, мы видим, что песок под ней и вокруг этого места через некоторое время снова становится влажным. Это происходит потому, что песок снова сокращается после удаления надавливающих сил и избыток воды выступает на поверхность".
Итак, песок не сжимается, а, наоборот, расширяется под ногой, а когда мы ее убираем, он вновь "сокращается". Это удивительное явление, обнаруженное физиком, могло бы быть предсказано математиком. Оно связано с проблемой так называемой "плотной упаковки равных сфер". А эта проблема, в свою очередь, тесно связана и с нашими многогранниками, и с нашими мозаиками.
На плоскости есть две возможности уложить круги: вписав их в квадратную и в шестиугольную мозаику. Интуиция подсказывает, а расчет подтверждает: второй способ позволяет уложить круги более компактно, как говорят, плотность упаковки тут выше. Можно доказать (это и сделал венгерский математик Ласло Фейеш Тот), что более плотной упаковки придумать невозможно.
Впрочем, открытие это совершено миллионы лет назад. Его коллективный автор - пчелы. (Взгляните еще раз на гравюру М. К. Эсхера "Метаморфозы. II". На ней вы увидите, как квадратная мозаика переходит в гексагональную - шестиугольную. "На этом месте,- пишет сам художник,- возникает ассоциация "шестиугольники - соты", и мысль эта поддерживается личинками, которые начинают шевелиться в каждой ячейке".)
Но в пространстве дело обстоит намного сложнее - вопрос о том, упакуются ли сферы, помещенные в трехмерные соты самым плотным образом, остается открытым. (То есть, поскольку центры их окажутся в вершинах куба, не ясно, является ли простая кубическая упаковка самой компактной.) У подножия старых военных памятников лежат обычно пушечные ядра в виде пирамиды - верхнее ядро покоится на четырех других, те, в свою очередь, на девяти ниже расположенных ядрах и т. д. Каждое попавшее внутрь пирамиды ядро касается двенадцати других - четырех в своем слое, четырех внизу и вверху. Это так называемая кубическая плотная упаковка, описанная Кеплером. Если положить пирамиду набок, то получится другой способ упаковки ядер-сфер, но плотность ее та же самая (точное ее значение 0,7408). Есть и еще варианты, но ни один не гарантирует самое компактное расположение.
(В том числе и тот, "икосаэдрический" (4), все из того же спора Ньютона с Грегори.).
Вопрос об упаковках - не праздный и не абстрактный. Он связан со строением вещества, его прочностью, а потому кровно интересует специалистов в разных областях науки.
Джон Десмонд Бернал, который был президентом Всемирного Совета Мира, крупный английский ученый, считал, например, что "текучесть жидкости есть результат ее молекулярной неоднородности".
И потому начались эксперименты.
"Земляника растет и под крапивой",- подметил Шекспир. Геометрическая мысль плодоносит и в худших условиях. "Я сдавливал свежий горох в одном и том же котле с силой в 1600, 800 и 400 фунтов,- писал еще в 1727 году Стефан Хейлс в своей "Статистике растений",- при этих опытах горох расплющивался, но его уровень не повышался, так как под действием большого веса масса гороха заполняла промежутки между горошинами, которые превращались в прелестные маленькие додекаэдры". Через двести с лишним лет, в 1939 году, опыт этот повторили два ботаника - Д. Марвин и Э. Мацке. Они заменили горошины свинцовыми пулями и увеличили давление в десять раз. Получились неправильные четырнадцатигранные тела. Грани были по преимуществу пятиугольными, хотя среди них встречались и четырех- и шестиугольные. Далее было обнаружено, что внутренние клетки растительных тканей тоже имеют в среднем четырнадцать граней. Исследовали под микроскопом пену, состоящую из двух тысяч пузырьков. Те шестьсот из них, что расположились в центре, имели в среднем по 13,7 касания с соседями, но чаще всего они превращались в тринадцатигранник, составленный из одного четырехугольника, двух шестиугольников и десяти пятиугольников. В 1959 году Джон Бернал изящнейшим образом показал, что пятиугольная грань действительно имеет преимущество перед другими. Он изготовил из пластилина массу одинаковых шариков, вывалял их в меловой пудре, а затем спрессовал в сплошной ком. У получившихся фигур в среднем было 13,3 грани, в большинстве своем пятиугольных.
И спрессованная случайная упаковка равных свинцовых пуль или пластилиновых шариков, и приблизительно однородная ткань, состоящая из растительных клеток, и пена, образованная примерно одинаковыми пузырьками, как бы стремятся приблизиться к трехмерным пространственным сотам, в которых число граней единичной ячейки находится где-то между пятью и шестью. Это "между", то есть дробное число граней, означает, что соты существуют в статистическом смысле: в каких-то ячейках четыре, в каких-то - пять, в каких-то - шесть граней.
Соты, то есть пространство, заполненное многогранниками, позволяют изучать пространственные фигуры, "находясь" между ними и миром плоскости. (Эта идея пришла в голову в 1897 году Форольду Госсету, молодому английскому юристу, который из-за отсутствия клиентов развлекался тем, что подсчитывал правильные фигуры, имеющие вид на жительство в четвертом, пятом, шестом и вообще любом измерении. Оказалось, что в четырехмерном пространстве их шесть, а в пяти - и более мерном живут лишь три правильных выпуклых многогранника - аналоги куба, тетраэдра и октаэдра. Правда, доказал это не Госсет, а Стрингхэм еще в 1880 году*. Но мысли Госсета о многомерных сотах математики не оценили, и скромный юрист вернулся к своим законам. Однако когда в журнале "Нейчур" в 1936 году появились стансы Ф. Содди "Поцелуй по расчету", где речь шла о "целующихся" многомерных сферах, Госсет откликнулся: он изложил в стихах часть тех выводов, что почти сорок лет пролежали в его архивах.) Соты помогли найти точную цифру, а именно 0,7797 (ее получил К. Роджерс в 1958 году), выше которой не может быть плотность ни одной упаковки. И в то же время очевидно, что любая меньшая плотность получается как бы сама собой, за счет случайных причин. Об этом и говорит эксперимент Осборна Рейнольдса на морском берегу: путешествуя по мокрому пляжу, мы изменяем упаковку песчинок, делая ее менее плотной, а такие варианты всегда, что называется, "под ногой". Под ударами волн или дождевых капель песчинки располагаются самым плотным из возможных способов. Теперь уже любое воздействие извне, особенно столь грубое, как давление ноги знаменитого ученого, не только не в силах уплотнить песок, но неизбежно разрушает "наиплотнейшеё" расположение песчинок, и потому вода засасывается в поры между ними. Рейнольде, разобравшись в сути явления, не советовал доверять продавцу, который, насыпав зерно в меру, начинает ревностно уминать его, как бы демонстрируя свое бескорыстие. На самом же деле при умелом уминании объем зерна может возрасти процентов на десять, а то и больше.
* (Это если считать по дате опубликования работы. Но Людвиг Шлефли получил то же доказательство раньше. Его рукопись долго пролежала в университетах Лейпцига и Берна и была опубликована лишь а 1901 году, через шесть лет после смерти автора.)
Еще нагляднее иллюстрирует тот же принцип трюк, проделываемый индийскими факирами. Они, тихонько потряхивая, наполняют кувшин с узким отверстием невареным рисом, а затем несколько раз погружают в него нож - как можно глубже. На десятый-одиннадцатый раз нож вдруг, на удивление всем, не ведающим о наиплотнейших упаковках, застревает, и факир с торжеством держит на нем весь сосуд!
Но, пожалуй, наиболее эффектен фокус, который сумели продемонстрировать сотрудники Научно-исследовательского института железобетона И. Г. Людковский и Ю. С. Волков. Колонны и опоры, придуманные ими, намного прочнее, чем любые из до сих пор известных строителям. Они словно сделаны из специальных дорогих сплавов. А на самом деле их конструкция представляет собой длинную спираль, свитую из проволоки, внутри которой насыпаны шары из стекла или каменного литья. Промежутки между шарами заливают бетоном. Как совершенно правильно пишут авторы сверхпрочной колонны в февральском номере журнала "Бетон и железобетон" за 1971 год, "при свободной укладке шары располагаются компактно, по так называемой кубооктаэдоической системе, когда один шар соприкасается с двенадцатью другими. Заполнение объема шарами составляет 74 процента". То есть одно из уже известных нам расположений пушечных ядер с плотностью 0,7408.
Оказывается, ни материал самих шаров (их можно делать из стекла, камня, шлакоситалла), ни исполнение окружающей их спиральной обоймы (Людковский и Волков предлагают заменить прочную проволоку стеклопластиковой арматурой, которая, кстати, устойчива против коррозии), ни, наконец, состав заполняющего промежутки между шарами раствора (марка бетона) не слишком сильно влияют на прочность колонны. Одна лишь геометрия превращает хрупкое стекло в безотказный металл, многотонным нагрузкам противостоит одна лишь сила математической мысли.
"Мой дом построен по законам самой строгой архитектуры. сам евклид мог бы поучиться, познавая геометрию моих сот",- говорит пчела в "Тысяче и одной ночи". Она права: пчелиная ячейка представляет собой нижнюю половину ромбододекаэдра, одного из полуправильных архимедовых тел, и это решение с точки зрения экономии воска и строительных усилий настолько разумно, что в академических кругах Франции возникла научная дискуссия, итог которой подвел Бернар Фонтенель, заявив, что за пчелами нельзя признать геометрического мышления на уровне Ньютона и Лейбница (хотя они и рассчитывают свои постройки в полном соответствии с открытым этими учеными дифференциальным исчислением и вытекающим из него принципом минимума), но они используют достижения высшей математики, подчиняясь божественному указанию и руководству.
Строители и архитекторы издавна предпочитают геометрические соображения даже самым очевидным и убедительным фактам. Они, например, пренебрегают заветом предков и с охотой строят дома на песке. Более того, если грунт не вызывает у них доверия, они выбрасывают его прочь и привозят на это место песок, который затем утрамбовывают. После объяснений Рейнольдса ясно, что песчинки приходят в состояние наиплотнейшего расположения и грунт приобретает все свойства твердого тела. Именно поэтому до сих пор прочно стоит "твердыня власти роковой" - Петропавловская крепость, первое большое архитектурное сооружение, построенное на песке - и на геометрической идее, заложенной в ее фундамент.
"Есть тонкие, властительные связи",- говорил поэт. Связь между правильными многоугольниками, мозаиками и многогранниками слишком глубока, чтобы не быть явной - они дети одной и той же математической идеи. Как плоскость можно покрыть некоторыми из правильных многоугольников, так и пространство удается заполнить Платоновыми телами. Случай с кубами тривиален. Но взгляните на гравюру Маурица Эсхера "Плоские черви", которой он предпослал такие слова: "Строительный кирпич имеет форму прямоугольного параллелепипеда, и это логично, потому что такие кирпичи соединять друг с другом проще всего. Но любой человек, любящий и понимающий красоту правильных тел, может пожалеть, что строители не используют другие формы. Например, тетраэдры, перемежающиеся с октаэдрами, могут складываться один с другим не хуже традиционных кирпичей. Вот дом, построенный из комбинаций этих двух форм. Он не имеет ни вертикальных, ни горизонтальных поверхностей, ни полов, ни стен, ни потолка - в обычном понимании этих слов. Вот почему он весь внутри заполнен какой-то жидкой средой, в которой плавают существа, напоминающие плоских червей - планарий".
Эти плоские черви вновь возвращают нас к мозаикам - обитателям двумерного мира.
Евклидову плоскость можно покрыть квадратами так, чтобы в каждой вершине их сходилось по четыре,- это и будет мозаика {4,4}. Но стоит нам захотеть объединить квадраты таким образом, чтобы к каждой вершине прилегало лишь три из них, как фигура замкнется в пространстве и мы получим куб {4,3}. Точно так же плоскость удается заполнить правильными треугольниками, собранными по шестеркам в каждой вершине,- мозаика {3,6}. Но если надо, чтобы вершину окружали три, четыре или пять таких треугольников, то мы опять получим замкнутые пространственные тела - уже знакомые нам тетраэдр {3,3}, октаэдр {3,4} и икосаэдр {3,5}.
Размышляя об этих превращениях, мы постигаем простейшие понятия топологии. И вместе с тем становится ясным, насколько общи ее законы, насколько универсален характер изучаемых ею зависимостей.
Первым, кто увидел глубокую общность мозаик и многогранников, был Иоганн Кеплер. Именно он предложил рассматривать плоскость, заполненную прилегающими друг к другу многоугольниками, как выродившийся многогранник и потому смог применить к ним одну и и ту же общую теорию.
Потом эта его мысль была продолжена в обе стороны: жалкая многократно "надломленная" прямая линия стала выродившимся многоугольником, а многогранники превратились всего лишь в трехмерных представителей неких многомерных сверхтел - величественных "политопов", речь о которых впереди.
Что же касается великолепных сферических мозаик, то их положение в известном смысле промежуточное - от плоскости ушли, а к многогранникам не пришли. Но именно поэтому они оказались очень удобным инструментом для исследования пространственных фигур. Кроме того, благодаря своей броской красоте они были изучены давно - первым их описывал известный на Востоке математик Абу-л-Ваф, живший в X веке. И в наши дни сферические мозаики притягивают к себе внимание художественных натур. Например, эсхеровские "Буковый шар", "Ангелы и дьяволы" и "Сфера с человеческими фигурами" - ювелирно вырезанные из дерева пространственные мозаики так хороши, что легко могут стать источником вдохновения и фантазии.
Сферическая мозаика
И то и другое нам понадобится, когда речь пойдет о фигурах, живущих в четвертом и более высоких измерениях,- сверхмногогранниках.
Высшее назначение математики -
находить порядок в хаосе,
который нас окружает.
Норберт Винер
С благодарностью к источнику: Библиотека по математике. Геометрическая рапсодия
The post Мировая гармония first appeared on Математику в помощь.
]]>частоте всего на одно колебание в секунду, т. е. почти 4000 звуков!).
The post Пропорции музыкальной гаммы first appeared on Математику в помощь.
]]>Пройдут миллионы лет, и если музыка в нашем смысле будет еще существовать, то те же семь основных тонов нашей гаммы, в их мелодических и гармонических комбинациях, оживляемые ритмом, будут все еще служить источником новых музыкальных мыслей.
П. Чайковский
Если окинуть взглядом 2500 лет истории европейской музыки, от Пифагора и до наших дней, то слова П. И. Чайковского, вынесенные в эпиграф, обретают особый смысл. В самом деле, каких только переворотов в мировоззрении, сознании и бытии человечества не произошло за это время! Но основа музыки - музыкальная гамма - остается практически неизменной. Музыкальная гамма даже в наш бурный век представляется незыблемым утесом в клокочущем море новых идей и теорий.
Но в чем причина такого завидного долголетия музыкальной гаммы? Почему из всего обилия звуков с частотой от 16 до 20000 Гц, которые способно воспринимать наше ухо (в области до 4000 Гц мы отличаем звуки, отстоящие друг от друга по частоте всего на одно колебание в секунду, т. е. почти 4000 звуков!), в музыке используется всего 7 октав по 12 звуков, т. е. всего 84 звука*?
* (Для педантов уточним, что концертный рояль имеет до 90 клавиш (звуков). )
Объяснить, почему музыкальный звукоряд содержит именно 7 октав, нетрудно. В самом деле, возьмем самую нижнюю ноту звукоряда - ля - субконтроктавы, частота которой равна 27,5 Гц, т. е. находится у нижней границы слышимости звуков. (Подходить ближе к границе слышимости не стоит, так как у каждого человека она своя и, значит, некоторые люди не услышат более низкие звуки.) Рассмотрим 8 октавных повторений этой ноты:
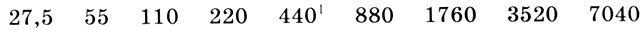
* (Частота ноты ля первой октавы - 440 Гц - является эталонной при настройке фортепиано и проверяется по камертону. Относительно этой ноты сохранилось интересное предание: в Древнем Египте около города Фивы находилась огромная статуя эфиопского Царя Мемнона. Статуя была повреждена во время землетрясения и каждое утро на рассвете якобы издавала звук ля,, который считался голосом Мемнона. Фивские музыканты приходили к статуе настраивать свои инструменты. К сожалению, в начале нашей эры голос Мемнона звучать перестал и проверить правоту предания невозможно.)
Легко видеть, что восьмая октава выходит далеко за границу четкой различимости высоких звуков (4000 Гц), и, таким образом, в диапазоне до 4000 Гц укладывается чуть более 7 октав. Выходить же за границу 4000 Гц нет смысла, так как звуки там плохо различаются по высоте и мелодия будет теряться.
Итак, в диапазоне от 16 до 4000 Гц укладывается чуть более 7 октав. Октав-ные звуки воспринимаются как подобные, родственные (это объясняется, как мы уже знаем, совпадением большого числа их гармоник) и служат своего рода масштабными метками в музыкальной шкале. Следовательно, построение музыкальной шкалы сводится к искусному делению октавы на составные части.
Почему октава разделена именно на 12 частей, мы уже объяснили в предыдущей главе. Как показала история развития музыки, только при таком делении октавы достигается та "строгая соразмеренная гармония всех частей, объединяемых тем, чему они принадлежат,- такая, что ни прибавить, ни убавить, ни изменить ничего нельзя, не сделав хуже". Эти слова являются определением красоты по Альберти. Красота же вечна. Таким образом, именно в пропорциональном гармоничном делении октавы на составные части и заключается источник красоты музыкальной гаммы, а значит, и секрет ее трехтысячелетнего долголетия.
Мы уже отмечали некоторые пропорции музыкальной гаммы. Мы также знаем, что пропорциональность и симметрия являются объективными признаками красоты. Однако чем ближе всматриваешься в музыкальную гамму, тем полнее раскрываются все новые закономерности ее пропорционального строения, а значит, и объективные законы ее красоты. Остановимся подробнее на некоторых из этих закономерностей.
Рассмотрим вначале равномерно-темперированную 12-ступенную хроматическую гамму, имеющую наиболее простое строение:
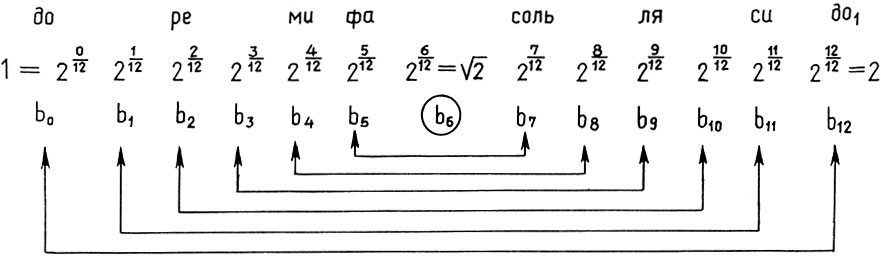
(11.1)
Легко видеть, что ступени равномерно-темперированной гаммы (11.1) образуют геометрическую прогрессию со знаменателем 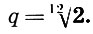 . Тогда
. Тогда
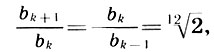 или
или 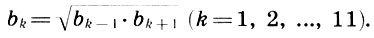 (11.2)
(11.2)
Следовательно, каждая внутренняя ступень гаммы (11.1) является средним геометрическим своих соседей. Назовем это локальной геометрической симметрией с коэффициентом симметрии (отношением входящих в пропорцию членов) 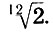 .
.
Кроме того, гамма (11.1) обладает глобальной геометрической симметрией, т. е. произведения членов (11.1), равноудаленных от концов, равны квадрату среднего члена b6:
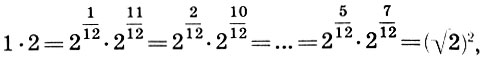
или 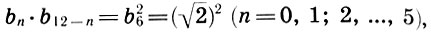 откуда имеем
откуда имеем
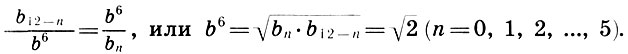 (11.3)
(11.3)
Таким образом, седьмая ступень (11.1) b6=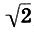 , так называемый тритон, равный увеличенной кварте или уменьшенной квинте, является средним геометрическим любой пары равноудаленных от концов ступеней. Назовем тритон b6=
, так называемый тритон, равный увеличенной кварте или уменьшенной квинте, является средним геометрическим любой пары равноудаленных от концов ступеней. Назовем тритон b6=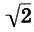 , центром глобальной геометрической симметрии гаммы (11.1). Глобальная геометрическая симметрия связывает интервал и его обращение через интервальный коэффициент октавы.
, центром глобальной геометрической симметрии гаммы (11.1). Глобальная геометрическая симметрия связывает интервал и его обращение через интервальный коэффициент октавы.
Если прологарифмировать (11.1) - (11.3) по основанию 2, то эти соотношения примут наиболее простой вид
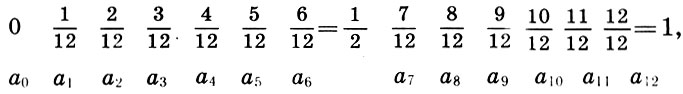 (11.4)
(11.4)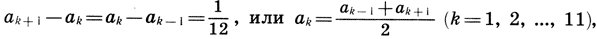 (11.5)
(11.5)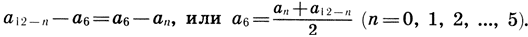 (11.6)
(11.6)Здесь ak = log2bk (k = 0, l, 2, ..., 12). Равенства (11.4) - (11.6) выражают тот простой факт, что логарифмическая октава [0; 1] разбита на 12 равных частей. Поэтому каждые три соседних члена (11.4) симметричны относительно среднего из них и отстоят от него на расстояние 1/12 (локальная симметрия), а середина логарифмической октавы а6=1/2 является центром ее глобальной симметрии, т. е. для каждого аn слева от а6 существует симметричный относительно а6 член a12-n справа от а6, так что расстояния a12-n - а6 и а6 - аn равны (n = 0, 1, 2, ..., 5).
Из равенств (11.1-3) или (11.4-6) очевидно, что при любых сдвигах (геометрических для (11.1) или арифметических для (11.4) структура равномерно-темперированной гаммы не нарушается, т. е. равномерно-темперированная гамма допускает модуляции в любые тональности. Эти возможности равномерной темперации, как отмечалось в главе 9, блестяще проиллюстрировал И. С. Бах в своем "Хорошо темперированном клавире".
Рассмотрим теперь лидийскую гамму пифагорова строя, или натуральный мажор (8.1), взяв в качестве дополнительных ступеней пониженные звуки (ре-бемоль, ми-бемоль, соль-бемоль, ля-бемоль, си-бемоль) и один повышенный звук (фа-диез) согласно (8.2):
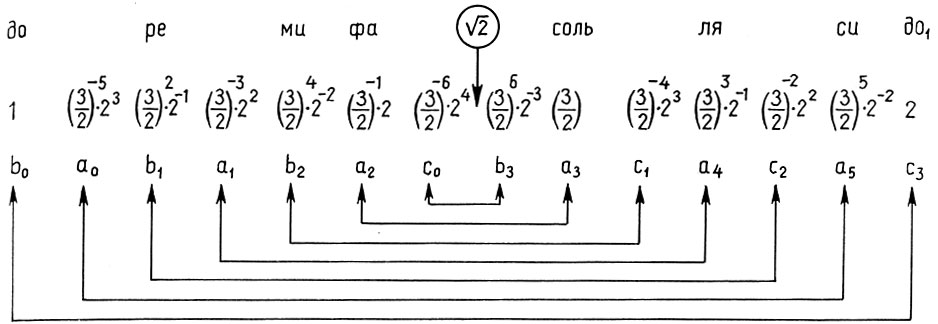 (11.7)
(11.7)
Структура пифагоровой гаммы (11.7) значительно сложнее. Однако при ближайшем рассмотрении можно обнаружить, что пифагорова гамма состоит из трех геометрических прогрессий, переплетенных между собой, подобно Платонову гептахорду (7.1), причем все три прогрессии имеют одинаковый знаменатель 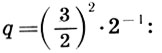 :
:
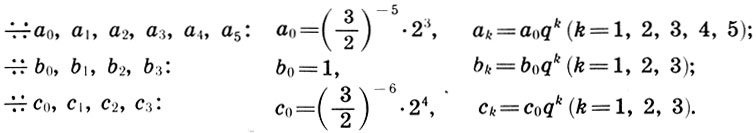
Для этих прогрессий справедливы соотношения
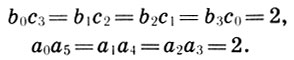
Учитывая расположение членов прогрессии в (11.7), приходим к выводу, что пифагорова гамма, также обладает глобальной геометрической симметрией. Следовательно, 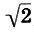 является центром глобальной симметрии пифагоровой гаммы.
является центром глобальной симметрии пифагоровой гаммы.
Но 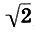 не является ступенью гаммы (11.7). Кроме того, в (11.7) осталась одна пара энгармонически неравных звуков соль-бемоль и фа-диез. Если в качестве энгармонически равного звука для соль-бемоль
не является ступенью гаммы (11.7). Кроме того, в (11.7) осталась одна пара энгармонически неравных звуков соль-бемоль и фа-диез. Если в качестве энгармонически равного звука для соль-бемоль 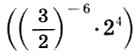 и фа-диез
и фа-диез 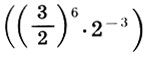 взять их среднее геометрическое
взять их среднее геометрическое 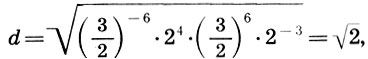 , то оно оказывается в точности равным центру глобальной симметрии
, то оно оказывается в точности равным центру глобальной симметрии 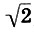 . Таким образом, мы получим 12-ступенную хроматическую пифагорову гамму с центром глобальной симметрии
. Таким образом, мы получим 12-ступенную хроматическую пифагорову гамму с центром глобальной симметрии 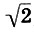 на седьмой ступени:
на седьмой ступени:
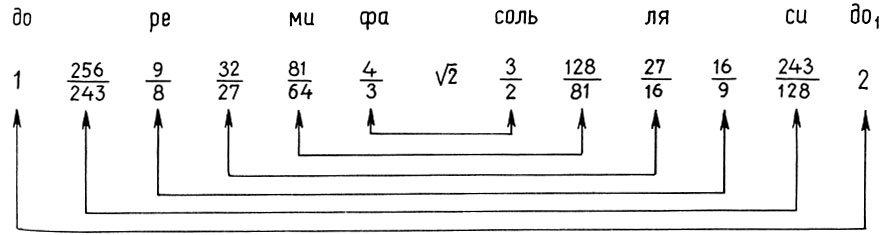 (11.8)
(11.8)
Легко проверить, что в гамме (11.8) можно взять чистые квинты на всех ступенях, кроме седьмой (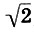 ), которая даст "волчью" квинту. Кроме того, сам интервал тритона (
), которая даст "волчью" квинту. Кроме того, сам интервал тритона (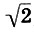 ), как мы знаем, является резким диссонансом. Оба этих качества составили тритону печальную славу. В средние века тритон называли "дьяволом в музыке", и до XVI века употреблять его в церковных песнопениях строго запрещалось.
), как мы знаем, является резким диссонансом. Оба этих качества составили тритону печальную славу. В средние века тритон называли "дьяволом в музыке", и до XVI века употреблять его в церковных песнопениях строго запрещалось.
Рассмотрим теперь диатоническую 7-ступенную гамму чистого строя (8.7):
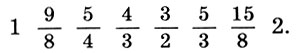 (11.9)
(11.9)Мы знаем, что гамма чистого строя является наиболее благозвучной, а ее интервальные коэффициенты имеют самый простой вид. Но еще удивительнее то, что гамма (11.9) является и самой пропорциональной. В самом деле, среднее арифметическое и среднее гармоническое основного тона (1) и октавы (2) дают нам квинту и кварту:
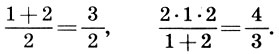
Среднее арифметическое и среднее гармоническое основного тона и квинты образуют большую и малую терции:
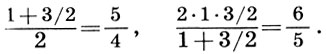
Наконец, взяв среднее арифметическое и среднее гармоническое основного тона и большой терции, мы получим оба интервала тона чистого строя:
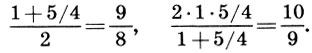
Таким образом, все главные интервалы чистого строя получаются как последовательная цепь средних пропорциональных, началом которой является пропорциональное деление октавы на квинту и кварту.
Перейдем к хроматической гамме чистого строя. Для построения дополнительных ступеней хроматической гаммы отложим полутон чистого строя (16/15) вверх от 1, 2, 4, 5 и 6-й ступеней диатонической гаммы (11.9), т. е. умножим их интервальные коэффициенты на 16/15, а также из соображений симметрии отложим полутон вниз от 5-й ступени. В результате получим 13-ступенную гамму:
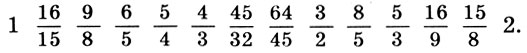
Интервальные коэффициенты 45/32 и 64/45 можно заменить на более простые 7/5 и 10/7, которые приближенно им равны 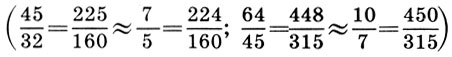 и также обладают геометрической симметрией относительно
и также обладают геометрической симметрией относительно 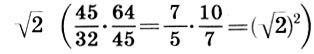 . В результате входящие в хроматическую гамму чистого строя интервальные коэффициенты выразятся с помощью отношения натуральных чисел, не превосходящих 16, которые можно трактовать как частоты первых 16 гармоник основного тона (1), или первые 16 ступеней натурального звукоряда:
. В результате входящие в хроматическую гамму чистого строя интервальные коэффициенты выразятся с помощью отношения натуральных чисел, не превосходящих 16, которые можно трактовать как частоты первых 16 гармоник основного тона (1), или первые 16 ступеней натурального звукоряда:
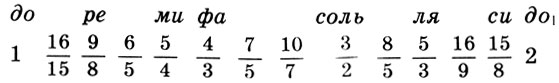 (11.10)
(11.10)
Заметим, что, как и в диатонической гамме (11.9), интервальные коэффициенты хроматической гаммы (11.10) не содержат 11-й и 13-й обертоны, а печально известный "фальшивый" 7-й обертон входит только в два коэффициента (7/5 = 1,4 и 10/7≈1,428), которые приближенно равны интервальному коэффициенту тритона 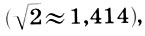 чья дурная слава известна в музыке не менее.
чья дурная слава известна в музыке не менее.
Взяв, как и в (11.8), в качестве энгармонически равного звука для соль-бемоль (7/5) и фа-диез (10/7) их среднее геометрическое 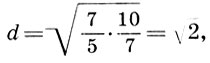 , мы придем к 12-ступенной хроматической гамме чистого строя интервальные коэффициенты которой имеют вид
, мы придем к 12-ступенной хроматической гамме чистого строя интервальные коэффициенты которой имеют вид
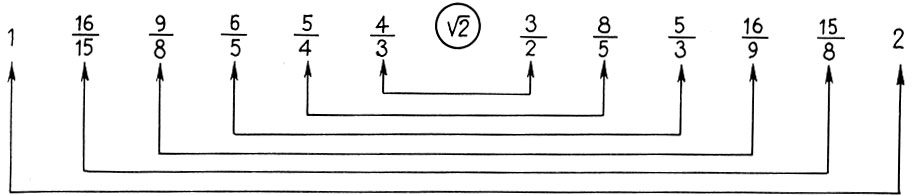 (11.11)
(11.11)
На этот раз интервальные коэффициенты в (11.11) не образуют никаких прогрессий. Однако, нетрудно обнаружить, что гамма (11.11) также обладает глобальной геометрической симметрией относительно 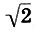 , т. е.
, т. е.
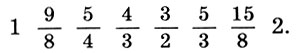
Гаммы (11.8) и (11.11) не обладают локальной геометрической симметрией, поэтому не допускают сдвигов без искажений. Последнее означает, что модуляции в другие тональности в пифагоровом и чистом строе затруднены.
Подведем некоторые итоги. Прежде всего мы видим, что музыкальные гаммы представляют собой строго упорядоченную совокупность звуков, отобранную из всего многообразия звуков, которые способно воспринимать и различать человеческое ухо. Именно закономерное построение гаммы, а следовательно и лада, позволяет на ее основе составлять и более сложные музыкальные конструкции, также носящие закономерный характер и называемые мелодией. Можно сказать, что гамма есть основная мелодия лада.
Отметим еще одно важное обстоятельство. В каждой из рассмотренных нами хроматических гамм: равномерно-темперированной (11.1), пифагоровой (11.8) и чистого строя (11.11) - точно выполнен один тип симметрии и только приблизительно другой. Так, равномерно-темперированная гамма (11.1) обладает локальной и глобальной геометрической симметрией, но в ней только приблизительно соблюдены пропорции деления октавы на квинту и кварту, большую и малую терции и т. д. Пифагорова гамма и гамма чистого строя обладают глобальной геометрической симметрией, но локальная симметрия в них выполнена только приблизительно. Зато в обеих гаммах точно соблюдено условие пропорционального деления октавы на квинту и кварту, а гамма чистого строя обладает еще двумя парами пропорций деления, что, видимо, и делает ее наиболее мелодичной из всех трех типов гамм.
Таким образом, в строении гаммы наряду с точной симметрией мы находим и приблизительную симметрию. Следовательно, в законах построения музыкальной гаммы отражается противоборство симметрии и асимметрии, олицетворяющих покой и движение, закономерное и случайное, вечное и сиюминутное. Именно диалектическое единство двух противоположных начал - симметрии и асимметрии - наполняет гамму подлинной гармонией, является источником вечной красоты и юного изящества музыкальной гаммы.
Поисками математических закономерностей в музыке усиленно занимался московский композитор М. А. Марутаев. Еще в студенческие годы М. Марутаева занимала мысль найти объяснение принципам музыкальной формы и ладогармонического языка. Результаты многолетних изысканий М. Марутаева легли в основу развитой им теории качественной симметрии чисел, позволившей автору определить меру нарушения симметрии в музыкальной гамме.
На основании теории качественной симметрии чисел Марутаев строит концепцию "универсальной гармонии", т. е., проще говоря, пытается решить одну из вечных загадок: найти "формулу красоты", "универсальную гармонию", которую искали еще древние греки и которая связала бы воедино законы природы и законы искусства.
К сожалению, и на сегодня это фантастическая задача, ибо человечеству пока не известны ни единые законы природы, ни тем более законы искусства.
Вот почему у концепции Марутаева много как пылких сторонников, так и ярых противников. Мы не будем останавливаться на концепции Марутаева, которая во многом спорна, а местами и просто содержит математические огрехи (но у кого хватит смелости объявить себя специалистом и в науке, и в искусстве?!), а отметим лишь некоторые любопытные факты, установленные Марутаевым.
Вновь обратимся к гаммам. Прежде всего заметим, что, хотя мы все время говорили о 12-ступенных хроматических гаммах, мы везде фактически включали в рассмотрение 13-ю ступень (октавное повторение основного тона), которая на самом деле является 1-й ступенью следующей октавы. Если в гаммах (11.1), (11.8) и (11.11) октавное повторение основного тона не рассматривать, то получается действительно 12-ступенные музыкальные ряды, которые Марутаев называет качественными музыкальными рядами, поскольку они состоят из оригинальных качеств:
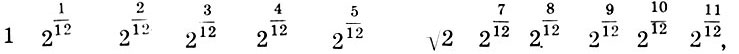 (1.12)
(1.12)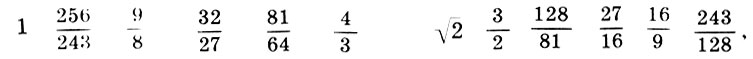 (1.13)
(1.13)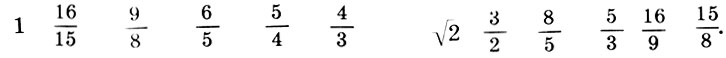 (1.14)
(1.14)
Легко видеть, что качественная равномерно-темперированная гамма (11.12) сохраняет свойство глобальной геометрической симметрии, центр которой сместился из точки 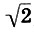 ≈1,41 в точку 211/24≈1,37:
≈1,41 в точку 211/24≈1,37:
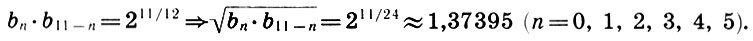
А вот для качественных гамм пифагорова и чистого строя глобальная геометрическая симметрия нарушится и будет выполняться только приблизительно. В самом деле, вычисляя среднее геометрическое для равноудаленных от концов членов ряда (11.13)
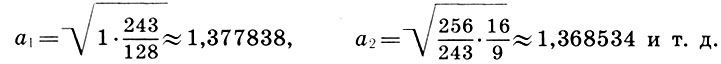
и ряда (11.14)
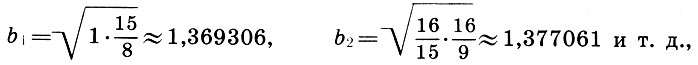
мы видим, что эти числа слегка различаются, однако их среднее арифметическое с точностью до 5 знаков совпадает между собой и с точностью до 4 знаков - 211/24
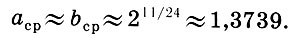
Итак, число 1,37 является центром глобальной геометрической симметрии (точной для (11.12) и приблизительной для (11.13) и (11.14)) 12-ступенных музыкальных гамм. Далее, Марутаев напоминает, что в ботанике известен идеальный угол расхождения листьев, равный 137°30'. Это математически рассчитанный угол, на который должны поворачиваться листья при их винтовом расположении вдоль стебля, так чтобы получать наибольшее количество вертикально падающего света. Удивительным оказывается и тот факт, что идеальный угол получается при двух последовательных делениях по золотому сечению угла 360°.
Особую роль играет число 137 и в физике, где оно является безразмерной комбинацией фундаментальных постоянных природы. Вот что по поводу этого числа пишет один из крупнейших современных физиков, лауреат Нобелевской премии англичанин Поль Дирак, возглавлявший в 60-е гг. XX века в Кембридже знаменитую лукасовскую кафедру - ту самую, которую в 60-е гг. XVII века профессор Исаак Барроу уступил своему 26-летнему ученику Исааку Ньютону: "В природе существует несколько фундаментальных констант: заряд электрона (е), постоянная Планка, деленная на 2π( =h/2π), и скорость света (с). Из этих фундаментальных констант можно вывести число, которое не обладает размерностью: с/е2. На основании экспериментальных данных установлено, что это число имеет величину 137 или весьма близкую к 137. Далее, нам неизвестно, почему оно имеет именно это значение, а не какое-нибудь иное. Для объяснения этого факта выдвигались различные идеи, однако никакой приемлемой теории не существует. Все же можно быть вполне уверенным в том, что физики когда-нибудь решат эту проблему и объяснят, почему это число имеет именно такое значение. Возможно, создадут такую физическую теорию, которая будет работать, если
=h/2π), и скорость света (с). Из этих фундаментальных констант можно вывести число, которое не обладает размерностью: с/е2. На основании экспериментальных данных установлено, что это число имеет величину 137 или весьма близкую к 137. Далее, нам неизвестно, почему оно имеет именно это значение, а не какое-нибудь иное. Для объяснения этого факта выдвигались различные идеи, однако никакой приемлемой теории не существует. Все же можно быть вполне уверенным в том, что физики когда-нибудь решат эту проблему и объяснят, почему это число имеет именно такое значение. Возможно, создадут такую физическую теорию, которая будет работать, если 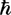 *с/е2 равно 137, и не будет работать, если оно имеет любое другое значение".
*с/е2 равно 137, и не будет работать, если оно имеет любое другое значение".
Еще один пример из физики. При распаде урана образуются осколки неравной массы. Кривая распределения осколков по массам имеет два максимума при массовых числах порядка 102 и 140 (это наиболее вероятные массовые числа осколков при распаде урана). Взяв отношение этих максимумов, имеем 140/102≈1,37.
Наконец, Марутаев приводит многочисленные примеры анализа музыкальных произведений по их метрическим параметрам, в которых встречается число 1,37. Рассматриваются сонатные или трехчастные формы. Протяженность музыкального произведения во времени можно характеризовать, например, числом восьмых долей или числом тактов, если размеры тактов (т. е. число восьмых долей в такте) не изменяются. Тогда протяженность трехчастной формы можно представить в виде Т = а + b + с, где а, b, с - числа тактов (восьмых долей) в экспозиции, разработке (средней части) и репризе соответственно. Оказалось, что во многих известных произведениях выдающихся композиторов: Моцарта (Соната № 12, ч. 1), Бетховена (соната № 14 "Лунная"), Дебюсси ("Детский уголок", пьеса № 1), Шостаковича (Фуга № 1, оп. 87) - имеет место соотношение
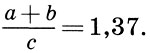
Так что же это такое: открытие "универсальной гармонии" или игра чисел? Почти наверняка - второе. Однако не нужно спешить обвинять автора в числовых спекуляциях. Вспомним кружочки противоположного цвета в мудром символе Ин-Ян: каждое доброе дело содержит крупицу зла и даже зло несет в себе частицу доброты. В нашем случае мудрый древнекитайский символ говорит: даже неправильная научная теория является шагом вперед на пути к истине.
Не нужно забывать' и исторический пример Пифагора, которого со всех сторон и во все времена обвиняли в числовых спекуляциях, но тем не менее сегодня общепризнано, что закон целочисленных отношений для консонансов является первым физическим законом, получившим математическое описание. Исследования Марутаева, безусловно, продвигают нас хотя бы на шаг вперед на трудном пути постижения математических тайн музыки. Впрочем, так их оценивает и сам автор. Что же касается "универсальной гармонии", то она представляется нам столь же непостижимой, как "абсолютная истина" или "перпетуум-мобиле".
С благодарностью к источнику: Библиотека по математике. Математика и искусство
The post Пропорции музыкальной гаммы first appeared on Математику в помощь.
]]>
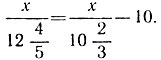
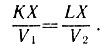
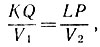 где V1 и V2 — постоянные числа
где V1 и V2 — постоянные числа
