Суммой векторов
и называется вектор
Для любых векторов справедливы равенства
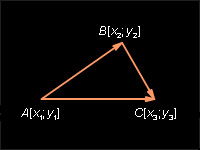
Каковы бы ни были три точки A, B и C, имеет место векторное равенство
Пусть A (x1; y1), B (x2; y2), C (x3; y3) –
Вектор имеет координаты вектор имеет координаты Следовательно, вектор имеет координаты Вектор имеет такие же координаты. По теореме 11.5 Теорема доказана.
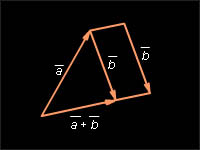
Замечание. Теорема 11.6 даёт следующий способ построения суммы произвольных векторов и Надо от конца вектора отложить вектор равный вектору Тогда вектор, начало которого совпадает с началом вектора а конец – с концом вектора будет суммой векторов и
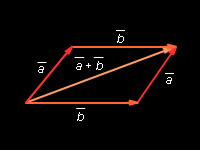
Правило параллелограмма: для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.
Разностью векторов и называется такой вектор который в сумме с вектором дает вектор откуда c1 = a1– b1; c2 = a2– b2.
Произведением вектора a ⟶ ( a 1 ; a 2 ) на число λ называется вектор т. е.
-
Для любого вектора
и чисел λ и μ
-
Для любых двух векторов
и
и числа λ
Абсолютная величина вектора
равна |λ || a|. Направление вектора
при
совпадает с направлением вектора
если
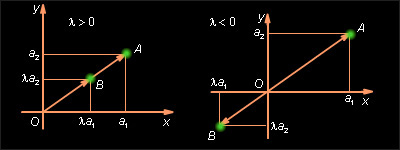
Построим векторы
и
равные
и
соответственно (O – начало координат). Пусть
и – координаты вектора
Тогда координатами точки A будут числа
и
координатами точки B – числа
и
Уравнение прямой OA имеет вид: αx + βy = 0. Так как уравнению удовлетворяют координаты точки A (a1; a2), то ему удовлетворяют и координаты точки
Поэтому, если λ > 0, то точка B лежит на луче OA, а следовательно, векторы и одинаково направлены. Если λ < 0, то точка B лежит на дополнительном луче и векторы и противоположно направлены.
Абсолютная величина вектора равна Теорема доказана.
Для любых отличных от нуля коллинеарных векторов и существует такое число λ, что
Пусть
и одинаково направлены. Векторы
и одинаково направлены и имеют одну и ту же абсолютную величину Значит, они равны:
Если векторы
и противоположно направлены, аналогично заключаем, что
Теорема доказана.
Пусть и – отличные от нуля неколлинеарные векторы. Любой вектор можно единственным образом представить в виде
Пусть A и B – начало и конец вектора Проведем через точки A и B прямые, параллельные векторам и Они пересекутся в некоторой точке C. Имеем Так как векторы и коллинеарны, то так как векторы и коллинеарны, то Таким образом,
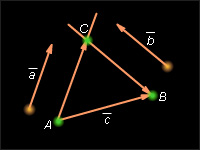
Для доказательства единственности представления допустим, что в условиях теоремы такое представление не единственно. То есть наряду с числами λ и μ такими, что существуют числа и такие, что и при этом верно хотя бы одно из соотношений Пусть для определенности Тогда из равенства имеем На основании теоремы 11.7 и замечания 11.1 получаем, что векторы и коллинеарны. Но это противоречит условию неколлинеарности этих векторов. Показанное противоречие доказывает единственность представления. Теорема доказана.
Скалярное произведение векторов.
Скалярным произведением векторов и называется число Скалярное произведение векторов и обозначется
Для любых векторов и верно:
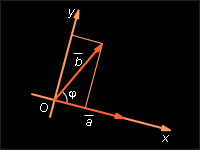
Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.
Пусть
и
– данные векторы и φ – угол между ними. Имеем:
Единичные векторы и имеющие направления положительных координатных полуосей, называются координатными векторами или ортами.
Любой ненулевой вектор единственным образом можно разложить по координатным векторам, то есть записать в виде
Так как координатные векторы отличны от нуля и неколлинеарны, то любой вектор допускает разложение по этим векторам в силу теоремы 11.9 Найдем λ и μ. Умножим обе части равенства скалярно на вектор Имеем С учетом того, что и ортогональны, имеем Аналогично, умножая равенство на получим или Таким образом, для любого вектора получается разложение Так как в силу теоремы 11.4 и теоремы 11.5 координаты однозначно определяют вектор, то разложение единственно. Теорема доказана.
С благодарностью к источнику: Открытая Математика. Планиметрия.
