Две прямые называются параллельными, если они не пересекаются.
Для обозначения параллельности прямых будем пользоваться символом ||.
Определяющее свойство задается аксиомой:
Через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну.
Для описания свойств параллельных прямых, вытекающих из определения и аксиомы 3.1, введем новые понятия и утверждения, связанные с взаимным расположением трех прямых на плоскости.
Прямая AC называется секущей по отношению к прямым AB и CD, если она пересекает обе прямые.
Если прямая AC является секущей по отношению к прямым AB, CD и, кроме того, точки B и D лежат в одной полуплоскости от секущей AC, то углы BAC и DCA называются внутренними односторонними.
Если AC – секущая по отношению AB и CD, а точки B и D лежат в разных полуплоскостях от AC, то углы BAC и DCA называются внутренними накрест лежащими.
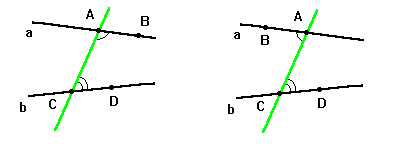
Если в данной паре внутренних накрест лежащих углов один из углов заменить на вертикальный ему, то полученные углы называются соответственными углами данных прямых с секущей.
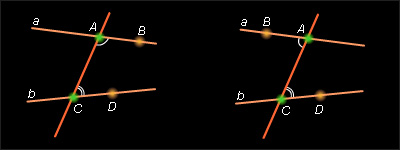
С благодарностью к источнику: Открытая Математика. Планиметрия.
