Совокупность полуплоскости и задающей ее прямой назовем замыканием полуплоскости, а прямую – границей полуплоскости.
Многоугольник называется выпуклым, если он лежит в замыкании одной полуплоскости относительно любой прямой, содержащей его сторону.
Определение выпуклости, данное в главе 9, эквивалентно для четырехугольника определению выпуклости главы 7.
Пусть четырехугольник является выпуклым в смысле определения главы 7 и O – точка пересечения диагоналей AC и BD. Рассмотрим произвольную пару смежных вершин четырехугольника (для определенности A и B) и прямую содержащую сторону AB. Точка O лежит в одной из полуплоскостей, задаваемых этой прямой. Тогда все точки лучей AO и OB лежат в замыкании этой полуплоскости и, в частности, точки C и D. Отсюда следует, что отрезки AC, CD, AB, BD также принадлежат замыканию одной полуплоскости, задаваемой прямой AB, а это и значит, что CD лежит в замыкании одной полуплоскости относительно прямой AB. Так как сторона AB была выбрана произвольно, то это верно для любой стороны и это завершает доказательство.
Пусть теперь верно определение выпуклости четырехугольника ABCD в смысле определения главы 9. В соответствии с этим четырехугольник ABCD лежит в плоском угле ABC, мера которого меньше 180°, с вершиной A и сторонами AB и AC, если прямая BD параллельна прямой AC, а прямая CD параллельна прямой AB, то ABCD – параллелограмм, а по теореме 7.5 его диагонали пересекаются, что доказывает утверждение. Пусть теперь одна из пар указанных прямых не параллельна, для определенности BD не параллельно AC.
Тогда, если M – точка пересечения BD и AC, то отрезок BM пересекает луч AD в точке D и AD лежит между сторонами угла BAC. Отсюда следует, что лучи AB и AC (за исключением вершины A) лежат в разных полуплоскостях от прямой AD и, следовательно, отрезок BC пересекает прямую AD в точке O, и более того, отрезок BC пересекает луч AD. Рассмотрим теперь угол BDC. По условию выпуклости ABCD лежит в плоском угле BDC, мера которого меньше 180°, аналогично можно доказать, что BC пересекает луч DA. Отсюда следует, что диагонали ABCD пересекаются и верно определение выпуклости в смысле главы 7.
Углом выпуклого многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в одной вершине. Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный углу многоугольника при этой вершине. Выпуклый многоугольник называется вписанным в окружность, если все его вершины лежат на некоторой окружности. Многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности.
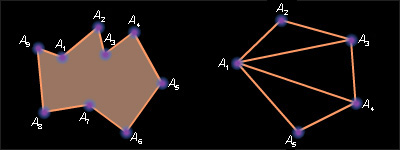
На рис. 9.2.1 слева показан пример замкнутой простой ломаной, которая образует невыпуклый многоугольник. Заштрихованная область – плоский многоугольник. Выпуклый многоугольник изображен на том же рисунке справа, [A1A3], [A1A4] – его диагонали.
Свойства выпуклого многоугольника.
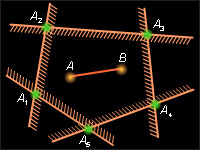
Отрезок, соединяющий любые две точки выпуклого плоского многоугольника (в частности, любая его диагональ), содержится в этом многоугольнике.
Пусть P – исходный выпуклый плоский многоугольник.
Возьмем две произвольные точки A и B, принадлежащие P. По определению P точки A и B лежат по одну сторону от любой прямой, содержащей сторону P, тогда [AB] также обладает этим свойством . Следовательно, [AB] содержится в P. Теорема доказана.
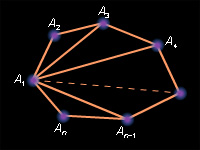
Выпуклый плоский многоугольник разбивается на треугольники всеми диагоналями, проведенными из одной (любой) его вершины.
Сумма углов выпуклого n-угольника равна 180° (n – 2).
В случае n = 3 теорема справедлива (теорема 4.8). Пусть A1A2... An – данный выпуклый многоугольник, и n > 3. Проведем все диагонали многоугольника из вершины A1. Они разбивают его на n – 2 треугольника: Δ A1A2A3, Δ A1A3A4, ... , Δ A1An – 1An. Сумма углов многоугольника совпадает с суммой углов всех этих треугольников. Сумма углов каждого треугольника равна 180°, а число треугольников – (n – 2). Поэтому сумма углов выпуклого n-угольника A1A2... An равна 180° (n – 2).
С благодарностью к источнику: Открытая Математика. Планиметрия.
