§4.6. Пропорциональные отрезки и средняя линия треугольника

Пусть пара параллельных прямых AB и CD пересекают соответственно другую пару параллельных прямых AC и BD. Тогда отрезок AC равен отрезку BD, а отрезок AB равен отрезку CD.
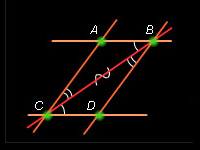
Пара параллельных прямых AB и CD пересекают другую пару параллельных прямых AC и BD
Рис. 4.6.1. К лемме 4.1

Проведём прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по первому признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. Лемма доказана.

Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
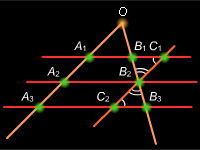
Доказательство Теоремы Фалеса
Рис. 4.6.2. Теорема Фалеса

Пусть A 3 O B 3  – заданный угол, а A 1 B 1 ,   A 2 B 2 и A 3 B 3  – попарно параллельные прямые и A 1 A 2  =  A 2 A 3 . Докажем, что B 1 B 2  =  B 2 B 3 Проведем через точку B 2 прямую C 1 C 2 , параллельную прямой A 1 A 3 По лемме 4.1 A 1 A 2  =  C 1 B 2 ,   A 2 A 3  =  B 2 C 2 и с учетом условия теоремы C 1 B 2  =  B 2 C 2 . Кроме того, ∠  B 1 C 1 B 2  = ∠  B 2 C 2 B 3  – как внутренние накрест лежащие при параллельных прямых A 1 B 1 ,    A 3 B 3 и секущей C 1 C 2 , а ∠  B 1 B 2 C 1  = ∠  C 2 B 2 B 3 , как вертикальные. По второму признаку равенства треугольников  Δ  B 1 C 1 B 2  = Δ  B 3 C 2 B 2 . Отсюда B 1 B 2  =  B 2 B 3 . Теорема доказана.

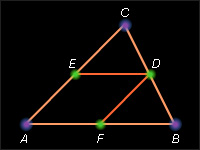
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна её половине.

Пусть [DE] – средняя линия в треугольнике ABC, т. е. AE = EC, CD = BD. Проведём через точку D прямую a, параллельную стороне AB. По теореме 4.11 прямая a пересекает сторону AC в её середине и, следовательно, содержит среднюю линию DE. Значит, средняя линия DE параллельна стороне AB. Проведём среднюю линию DF. Она параллельна стороне AC. Тогда по лемме 4.1 отрезок ED равен отрезку AF и равен половине отрезка AB. Теорема доказана.

Средняя линия треугольника
Рис. 4.6.3. Средняя линия треугольника

Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

Пусть стороны угла O пересекаются параллельными прямыми в точках B, D и A, C соответственно.

Теоремой утверждается, что OA OB = OC OD .

Разделим отрезок OD на n равных частей. Пусть δ1 – длина отрезка деления. Тогда OD = n ċ δ1.

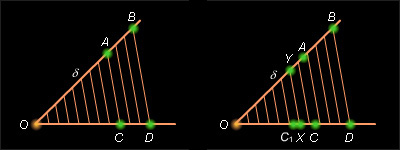
Параллельные прямые, пересекающие стороны угла
Рис. 4.6.4. К теореме 4.13

Возможны два случая.

  1. Существует такое n, при котором C – точка деления. То есть существует m < n такое, что OC = m δ1. Проведём через точки деления отрезка OD прямые, параллельные прямой BD. По теореме Фалеса эти прямые разбивают отрезок OB на равные отрезки некоторой длины δ 1 . Тогда OA = m δ 1 ,   OB = n δ 1 и OA OB = m δ 1 n δ 1 = m n ;    OC OD = m δ 1 n δ 1 = m n , т. е.  OA OB = OC OD .
  2. Ни при каком n, C не является точкой деления. Допустим, OA OB ≠ OC OD или без ограничения общности OA OB > OC OD . Отложим на луче OD отрезок O C 1 = OA OB ċOD<OC . Разобьём OD на n равных частей и проведем через точки разбиения прямые, параллельные BD. При достаточно большом n на отрезке C1C будет точка деления. Обозначим её через X, а соответствующую точку на стороне OB – через Y.

По доказанному OY OB = OX OD .

Заменим OY на большую величину OA, а OX – на меньшую величину O C 1 и получим OA OB > O C 1 OD или O C 1 < OA OB ⋅OD . Это противоречит построению отрезка O C 1 .

Теорема доказана.
С благодарностью к источнику: Открытая Математика. Планиметрия.